



L’esperienza non è ciò che ti succede. È ciò che fai con quello che ti succede
Somma, Differenza e Prodotto

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possaessere grande sia
la propria ignoranza!




Possiamo sommare numeri reali a numeri immaginari, ottenendo
oggetti del tipo (oppure ).
Per queste entità definiamo somma, prodotto e differenza sulla
scorta di quanto fatto in algebra per i binomi, ricordando la
proprietà di i prima enunciata.
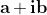
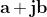
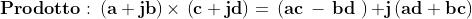
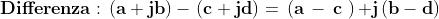
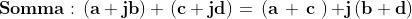
Con queste definizioni è possibile dimostrare che oggetti matematici come
godono effettivamente di tutte le proprietà caratteristiche dei numeri e quindi sono
da considerarsi numeri a tutti gli effetti.
Essi prendono il nome di numeri complessi.
Il numero a ( oppure c) è detto parte reale del numero complesso, mentre b (oppure
d) è la parte immaginaria. Se , allora ,parte reale di z e ,
parte immaginaria di z.
D'ora in avanti, per indicare un numero complesso useremo un carattere tipografico
in grassetto, oppure , carattere sopralineato
Esiste un numero complesso che sommato a qualsiasi altro numero complesso
, dia il numero z stesso?
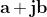
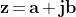
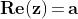
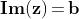
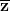
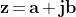
Sì, è , infatti :
Questo numero è l'elemento neutro per la somma di numeri complessi
Esiste un numero complesso che moltiplicato per qualsiasi altro numero complesso
, dia il numero z stesso?
Anche in questo caso la risposta è affermativa: questo numero è , infatti:
, è l'elemento neutro
per il prodotto di numeri complessi
Numeri complessi coniugati
Abbiamo visto prima che i2 = −1, per cui .
Questo è vero qualsiasi sia il numero immaginario. Esempio: i .
Numeri di questo tipo si dicono numeri immaginari coniugati.
Differiscono solo per il segno e moltiplicati tra loro danno sempre un numero reale
positivo, che è il quadrato della parte immaginaria del numero immaginario stesso:
.
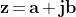
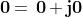
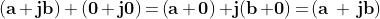
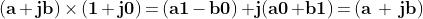
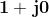
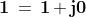
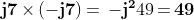
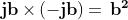
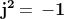
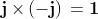
Generalizzando: ed sono numeri complessi coniugati.
Essi differiscono solo per il segno della parte immaginaria.
Se moltiplichiamo due numeri complessi coniugati tra loro otteniamo:
Qui abbiamo usato la proprietà commutativa: .
La radice quadrata di questa grandezza, sempre positiva, è detta modulo
del numero complesso.
Chiamando e , avremo quindi : .
Il complesso coniugato di , è indicato anche con .
Spesso il modulo è indicato con la lettera r:
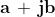
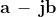

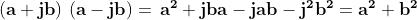
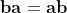
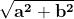
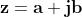
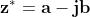
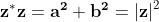
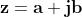
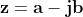
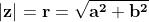
DIVISIONE
Leggermente più laboriosa è la procedura per la divisione tra numeri complessi:
Dovendo eseguire ad esempio:
per evitare la complicazione di un denominatore complesso, si sfrutta la proprietà
dei complessi coniugati e si assume che una frazione complessa (come una
frazione algebrica) non vari moltiplicando numeratore e denominatore per lo stesso
numero (complesso).
In questo caso moltiplicheremo numeratore e denominatore per il complesso
coniugato del denominatore:
ottenendo così un denominatore reale, che sappiamo facilmente trattare.
In seguito dimostreremo che è possibile elevare a potenza e estrarre radice dei
numeri complessi e che valgono tutte quelle proprietà (commutativa, associativa,
distributiva) che ci assicurano che i numeri complessi sono numeri a tutti gli effetti.
Definizione formale di numero complesso
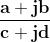
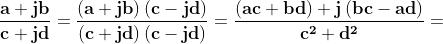
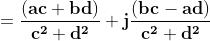
Vediamo ora una definizione formale di numero complesso
Definizione: I numeri complessi sono costituiti da coppie ordinate di numeri reali.
Tra tali coppie è definita un' operazione somma:
e un'operazione prodotto:
Date queste definizioni si può facilmente dimostrare che:
L'elemento neutro per la somma è ;
L'elemento opposto di è ;
L'elemento neutro per la moltiplicazione è
Il reciproco di un numero complesso , indichiamolo con , è:
Infatti, detto un numero complesso qualsiasi, e il suo reciproco, si deve
avere , cioè .
Per determinare r ed s basta allora risolvere il sistema
che dà appunto:
Possiamo quindi definire l'operazione divisione come prodotto
I numeri reali sono tutte le coppie del tipo con parte immaginaria nulla.
Tutte le coppie del tipo , cioè con parte reale nulla, rappresentano i numeri
immaginari.
Applicando le definizioni:
l prodotto di due numeri reali è un numero reale
Il prodotto di due numeri immaginari è un numero reale:
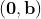
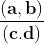
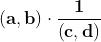
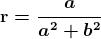
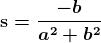
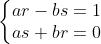
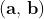
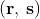
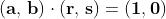
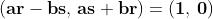
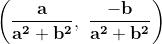
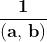
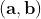
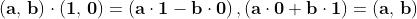
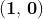
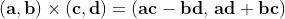
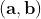
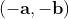
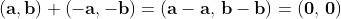
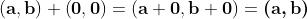
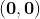
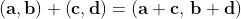
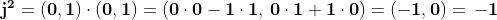
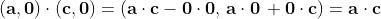



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



