



Anche un viaggio di mille miglia inizia con un singolo passo.
I Numeri Complessi

… studiare, studiare ed ancora
studiare, è il solo modo di capire
quanto possaessere grande sia
la propria ignoranza!





Introduzione e cenni storici
La prima fugace comparsa dei numeri complessi avviene
nella prima metà del XVI secolo, in Italia.
Autore di questa comparsa fu Gerolamo Cardano (1501-1576),
poliedrico medico e matematico, trattando del metodo della
falsa posizione, propone questo problema,manifestamente
impossibile :
"Dividi 10 in due parti che moltiplicate tra loro diano 40 "
Che possiamo anche enunciare così:
Trovare due numeri x e y, tali che x + y = 10 e x·y = 40.
Seguiamo per un momento il ragionamento di Cardano.
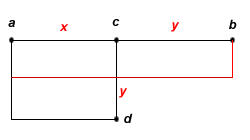
Immaginiamo che un segmento ab sia lungo 10 (non
importa l'unità di misura).
Il quadruplo del segmento ab, che potremmo rappresentare
con il rettangolo rosso, vale 40.
Il punto c divide ab in due parti x e y, il cui prodotto deve
dare 40. Inizialmente (falsa posizione) Cardano fa coincidere
c con il punto medio di ab e quindi x = y = x0 = 5.
L'area del rettangolo ad (così lo identifica), che in questo caso è un quadrato, è pari
a xy = x02 = 25, ovviamente diverso da 40.
La soluzione, se esiste, si può ottenere solo spostando c di una quantità r dalla
posizione iniziale, ma è chiaro che se, ad esempio, x diminuisce di r, allora y dovrà
aumentare della stessa quantità, cioè se x = x0 - r allora y= x0 + r.
Questo perchè la somma x +y deve essere uguale alla lunghezza di ab.
Se x = x0 − r e y = x0 + r sono la suddivisione cercata, dovrà essere vero che
(x0 − r)(x0 + r) = 40, nel caso specifico (5 − r)(5 + r) = 40.
Svolgendo il prodotto notevole (somma per differenza), si ha 25 − r2 = 40, il che
implica che r2 sia negativo:
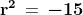
A questo punto Cardano introduce la quantità , da sottrarre e aggiungere a 5
per avere la soluzione cercata:
e
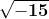
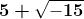
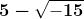
Quindi dimostra che effettivamente queste entità costituiscono una soluzione del
problema, dato che:
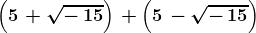
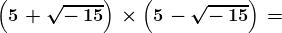
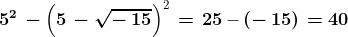
= 10
Ma Cardano, non riesce a trovare una giustificazione per queste strane quantità.
Ne attribuisce la comparsa alla diversa natura di ad (il quadrato), che non è la
stessa di 40 (che considera una linea), essendo una superficie più lontana dal
numero e una linea più vicina ad esso.
Alla fine, non riconoscendo il "tesoro matematico" che aveva a portata di mano,
ritiene questi ragionamenti essere capziosi (sofistici) e tanto sottili quanto inutili.
Radici quadrate negative comparivano anche nelle formule risolutive di alcune
equazioni di terzo grado:
ad esempio , di cui si conosceva, per sostituzione diretta, la radice
reale .
La formula risolutiva di Cardano dava:
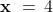
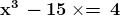
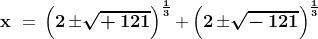
Raffaele Bombelli (1526-1573) cercò di dare alle radici cubiche della formula
precedente un'espressione formalmente simile a quella dei radicandi, quindi del tipo
.
Secondo la notazione moderna deve essere allora: e
.
Sapendo che si deve avere , si può facimente dimostrare che
Descartes detto Cartesio (1596-1650) per primo chiamò numeri immaginari entità
quali o ed
Eulero (1707-1783) nel 1777 introdusse il simbolo "i" per designare la radice
quadrata di , .
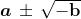
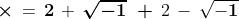
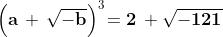
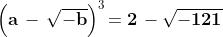
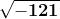
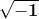
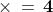
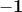
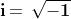
Ciò che sembrava quasi un incidente matematico, qualcosa in cui non credere
veramente (numeri immaginari in contrapposizione con i numeri reali), si è poi
rivelata una delle più feconde scoperte della Matematica.
Accade spesso così.
I numeri complessi, le strutture e i concetti matematici che da essi derivano sono
ora uno strumento irrinunciabile per la conoscenza scientifica e per la stessa
Matematica.
NUMERI IMMAGINARI
Se, nel campo dei numeri reali, tentiamo di risolvere equazioni come: ,
andiamo incontro ad una difficoltà insormontabile.
L'equazione infatti può essere scritta come , ma sappiamo che non esiste
alcun numero reale il cui quadrato sia negativo.
Non siamo in grado di eseguire l'operazione di estrazione di radice quadrata di
numeri negativi in campo reale, per cui una soluzione come viene
considerata priva di senso.
Per molto tempo si è evitato il problema semplicemente ammettendo che
l'equazione non possieda soluzioni in campo reale.
Il problema viene risolto introducendo la quantità , detta unità immaginaria.
Una prima evidente proprietà dell'unità immaginaria è la seguente:
Conseguentemente abbiamo anche: ed
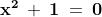
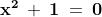
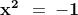
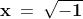
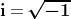
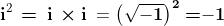
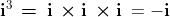
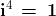
Daremo più avanti una interpretazione geometrica di questi risultati.
Le soluzioni della precedente equazione , sarebbero allora x1 = +i e x2 =
−i.
x2 + 4 = 0, ad esempio, darebbe come soluzioni e .
Oggetti di questo tipo prendono il nome di numeri immaginari e sono formati dal
'prodotto' di un numero reale per l'unità immaginaria stessa.
In realtà per affermare che si tratta di numeri bisogna provarlo, cioè si deve
verificare che siano soddisfatte le proprietà tipiche dei numeri.
In particolare deve essere possibile definire le operazioni che si possono eseguire
tra numeri, tra cui, ovviamente somma e prodotto.
Possiamo creare nuovi numeri immaginari sommando (o sottraendo) ripetutamente i
a se stessa: , o moltiplicando i per un numero reale: ,
, , ecc.
In generale sarà possibile sommare due numeri immaginari applicando le regole
algebriche per i monomi, così: . Analogo discorso per la moltiplicazione,
tenendo presente la proprietà di i prima enunciata: .
Questo può essere evidenziato affermando che il prodotto di due numeri immaginari
qualsiasi è sempre un numero reale.
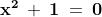
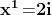
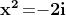
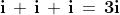
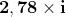
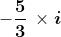
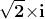
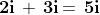
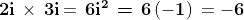


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



