



Anche un viaggio di mille miglia inizia con un singolo passo.
TANGENTE E COTANGENTE

… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!







Oltre a Seno e Coseno si usano anche altre funzioni da
loro derivate.
In particolare i quozienti di Seno e Coseno hanno un
nome proprio: Tangente e Cotangente:
Eccone la definizione:
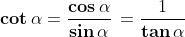
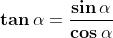
(1)
(2)
Si noti che queste due espressioni sono reciproche e quindi strettamente legate: il
loro prodotto è 1. (Su alcuni calcolatori tascabili manca il tasto per Cotangente, che
può essere calcolata come 1/Tangente). A volte invece di tan e cot si usano le
abbreviazioni tg e ctg.
A differenza di Seno e Coseno, per certi angoli Tangente e Cotangente non sono
definite:
Si provi ad esempio a calcolare tan(90°) oppure cot(0°).
Il nostro calcolatore ci da "Infinito", avvertendoci che è stata tentata una divisione
per zero .
Dalle definizioni (1) e (2) infatti deduciamo:
•
Se (cosa che si verifica quando oppure , dove l'ultimo
caso è equivalente a ), il denominatore in (1) diventa zero. In questi
casi dunque non è definita, mentre
•
Se (cosa che si verifica quando oppure ), il
denominatore in (2) diventa zero. In questi casi dunque non è definita,
mentre .
In tutti gli altri casi il nostro calcolatore ci fornisce dei numeri concreti che però
adesso possono essere grandi a piacere.
Anche Tangente e Cotangente possono essere interpretate come rapporti fra i lati in
un triangolo rettangolo. Per le definizioni finora date, deduciamo che
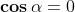
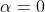
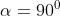
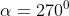
.
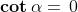
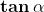
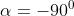
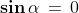
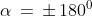
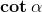
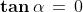

tan α = cateto opposto
cateto adiacente
cot α = cateto adiacente
cateto opposto


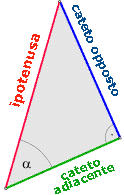
Come esempio applicativo consideriamo
il seguente problema geodetico:
La vetta di un monte alto 1.24 km viene
osservata sotto un angolo di 19.5°.
A che distanza si trova l'osservatore dalla
proiezione sul piano della vetta del
monte?
Soluzione: Osserva il triangolo rettangolo poco sopra ed usiamo la relazione :
(18)
Quindi
Usando il calcolatore otteniamo .
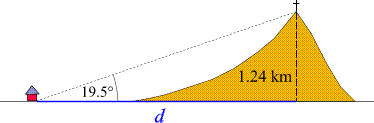
Dunque (dove per scopi pratici in genere sarà
sufficiente il valore approssimato
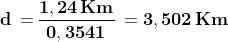
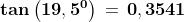
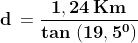
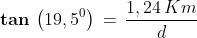
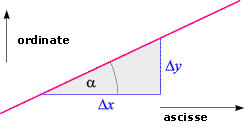
TANGENTE E COEFFICIENTE ANGOLARE
La Tangente ha un ruolo molto particolare poiché
esprime la relazione fra il coefficiente angolare e
l'angolo di pendenza di una retta.
Per determinare il coefficiente angolare di una
retta, si raffigura , come nel disegno a fianco,
il suo"triangolo di pendenza".
Il quoziente si chiama coefficiente angolare, ed ha il medesimo valore
in ciascun triangolo di pendenza, indipendentemente dalla sua grandezza.
La realazione (18) ci dice che il coefficiente angolare è uguale alla tangente
dell'angolo di pendenza che l'asse delle ascisse forma con la retta stessa:
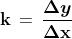
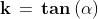
(20)
Se ad esempio l'angolo di pendenza di una strada misura 12°, il coefficiente
angolare è , che è circa pari a 0 .21.
Sul cartello stradale che indica la pendenza della strada troveremo scritto "21%"
(che possiamo leggere come "21 metri di dislivello per 100 metri di distanza percorsi
secondo la carta stradale").
Per una retta perpendicolare non ha senso parlare di coefficiente angolare, e ciò
corrisponde al fatto che e non sono definite.
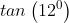
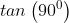
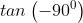
Proprietà di Tangente e Cotangente
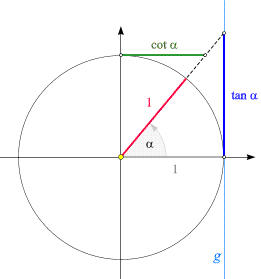
Le relazioni sopra elencate per Seno e Coseno implicano una serie di proprietà
utili per Tangente e Cotangente. Come per Seno e Coseno
possiamo utilizzare la circonferenza goniometrica,
come raffigurata qui a fianco.
L'angolo α è individuato dal raggio (rosso).
La Tangente di questo angolo corrisponde alla
lunghezza del segmento riportato sulla retta
azzurra g.
Per la relazione (20) essa è pari alla pendenza del
raggio, che nello schizzo è stato prolungato con
una linea tratteggiata fino a intersecare la retta g.
Anche per un angolo ottuso oppure negativo possiamo
individuare la tangente sulla stessa retta g.
Con questo metodo possiamo anche determinare facilmente il segno per un tale
angolo. Nei casi e il raggio è parallelo alla retta g.
Questa è la spiegazione geometrica del fatto che la tangente non è definita per
questi angoli.
Per la Cotangente valgono proprietà analoghe, scambiando i ruoli degli assi
cartesiani.
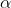
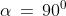
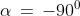
Angoli speciali
Per certi angoli i valori delle funzioni trigonometriche possono essere espressi con
le operazioni di calcolo usuali, in particolare con radici quadrate.
Riportiamo nella seguente tabella alcuni di questi angoli con i rispettivi valori:

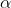
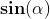
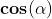
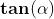
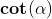




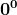
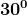
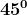
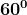
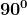
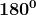
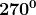
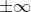
0
1


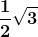
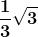
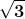
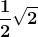
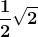
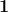





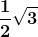

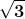
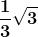

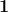
0
0
0
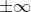



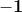
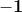
0
0
0
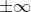
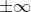
0
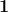
In tutte le frazioni che contengono radici quadrate abbiamo reso razionale il denominatore.
Il simbolo ±∞ sta a indicare che il valore corrispondente non è definito.
RADIANTI
Ci sono varie misure angolari, cioè sistemi per misurare un angolo. Il metodo che
probabilmente vi è più usuale è il sistema sessagesimale, che si basa sulla divisione
dell'angolo giro in 360 "gradi angolari".
Il numero 360 per l'angolo giro è scelto per motivi storici, ma dal punto di vista
matematico non é molto vantaggioso.
Per molti scopi è molto più utile passare a un altro sistema, la misura in radianti.
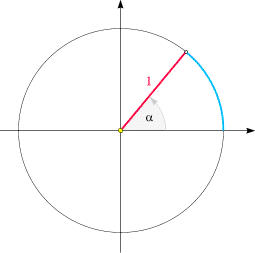
Qui la grandezza di un angolo si misura come lunghezza dell'arco corrispondente su
una circonferenza di raggio 1.
Ciò è rappresentato nella figura qui a fianco: Invece di misurare
l'angolo α in gradi, si usa la lunghezza dell'arco azzurro come
misura per la sua grandezza.
L'angolo giro in radianti è dato dalla circonferenza del cerchio
di raggio 1, cioè da 2B.
Esempio: Un angolo di 60° (cioè un sesto dell'angolo giro)
in radianti è pari a B/3, cioè circa 1.0472. Vediamo subito
gli svantaggi della misura in radianti: Angoli "rotondi" come
30°, 45°, 60°, 90°, 180° e 360° vengono rappresentati da
numeri irrazionali. Nella migliore delle ipotesi sono dati da
multipli razionali di B (come B/3 per 60°).
Quando un angolo è dato in radianti generalmente non si indica "l'unità di misura"
(cioè non si mette un simbolo come °). A volte si usa l'abbreviazione rad (ad
esempio 60° è B/3 rad, quindi circa 1.0472 rad), ma questo non è necessario.
La trasformazione da gradi in radianti e viceversa è molto semplice: Se è un
angolo dato in gradi, il suo valore in radianti è 2B × /360°. Viceversa un valore in
radianti va moltiplicato per 360°/(2B) per ottenere l'angolo in gradi.
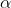
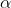
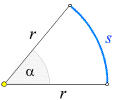
La misura in radianti di un angolo può essere anche individuata con
un cerchio di raggio arbitrario r.
Se, come nel disegno a fianco, l'arco ha lunghezza s, allora l'angolo α
in radianti è dato dal quoziente s/r. Per il cerchio di raggio 1 (r = 1)
ritroviamo la nostra definizione.
Questa proprietà deriva dal fatto che tutti gli "spicchi di torta" con lo stesso angolo
sono simili fra loro. Differiscono soltanto per la loro grandezza, ma il rapporto fra le
lunghezze s/r è costante per tutte queste figure, e può essere quindi usato come
misura dell'angolo.
Torniamo adesso alle funzioni trigonometriche. Alcune delle formule che abbiamo
visto si riferivano alla misura in gradi e possono ora essere tradotte in radianti. La
periodicità di Seno e Coseno in radianti sono date dalle formule:
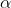
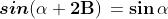
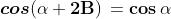
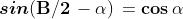
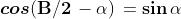
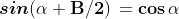
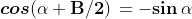
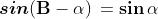
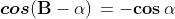
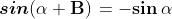
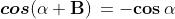
Anche le relazioni riguardanti Tangente e Cotangente e la tabella riportata sopra con
i valori delle funzioni trigonometriche per alcuni angoli speciali hanno una versione
analoga in radianti.
e quindi :



Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor



