



I libri migliori sono proprio quelli che dicono quel che già sappiamo
OTTICA TEORICA
TRASFORMATE DI FOURIER
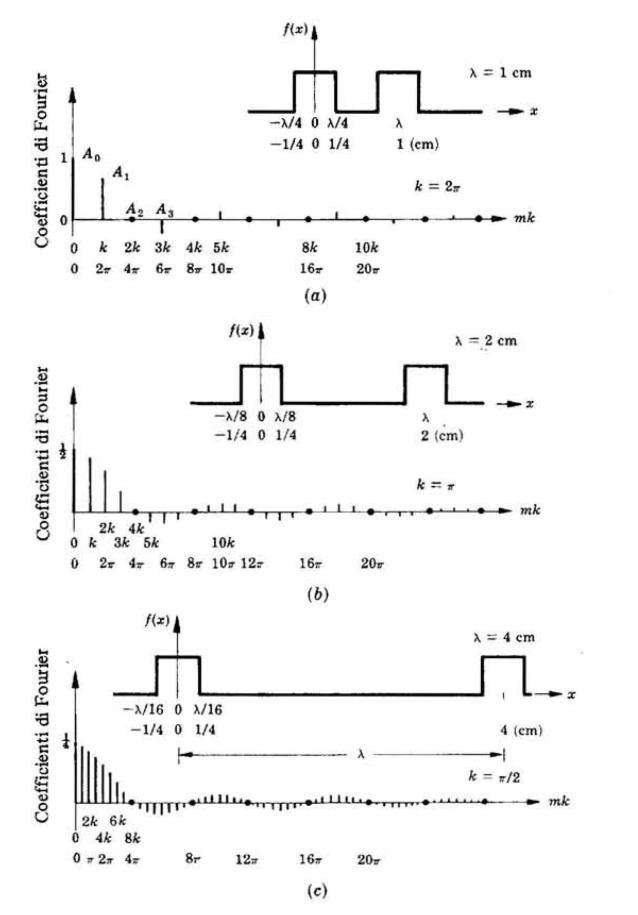
Si riconsideri per un momento l'onda quadra periodica vista in
precedenza e che mostriamo nuovamente a lato.
I coefficienti della serie di Fourier corrispondente, cioè gli
variano come una funzione sinc. Dato che questi termini sono
coefficienti di peso che determinano per ogni frequenza spaziale
quanto contribuisca al valore complessivo della funzione ognuna
delle componenti armoniche, un diagramma dei loro valori come
quello della ottostante figura, è detto spettro di frequenza.
Si noti nella figura che man mano che i picchi dell'onda quadra
si distanziano, essi rappresentano frazioni via via minori della
lunghezza d'onda, anche se la loro larghezza resta immutata.
Ora, man mano che i dettagli della funzione da riprodurre dive-
-ntano piccoli in rapporto a
, le componenti di Fourier devono a
loro volta avere lunghezze d'onda minori e di conseguenza
frequenze spaziali maggiori. Lo spettro della sottostante figura (c) mostra chiaramente
questo numero crescente delle componenti di frequenza.
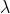
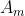
Se si fa tendere
ad infinito, con il che si ha un singolo impulso invece di una
funzione periodica, l'insieme discreto di frequenze spaziali, cioè tutti i valori mk, tendono
a formare una distribuzione continua.
La rappresentazione in serie di Fourier della funzione periodica si trasforma nell'integrale
di Fourier per una funzione non periodica:
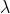
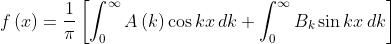
dove
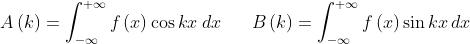
Le ultime due grandezze sono note come trasformate coseno e trasformate seno di
Fourier della funzione f(x)
Anche in questo caso si può introdurre una rappresentazione complessa conveniente:
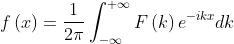
dove
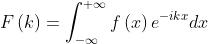
La funzione è detta trasformata di Fourier della funzione e si scrive
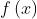
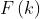
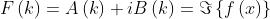
Adottando una scrittura analoga per le trasformate coseno e seno si ha
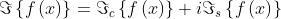
La grandezza f(x) è detta antitrasformata di Fourier di F(k) e si scrive
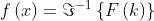
Nel contesto degli argomenti trattati , l'interesse maggiore alla coppia di Fourier,
f(x) e F(k), riguarda proprio la trasformata, più che il procedimento di sviluppo in
serie della funzione stessa.
Tuttavia dato che le funzioni di maggior interesse sono in questo contesto
bidimensionali nello spazio, conviene generalizzare la trasformata di Fourier nel
modo seguente:
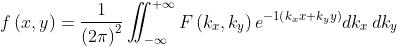
e
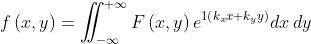
In una precedente pagina, si è visto che nel caso di Fraunhofer il campo diffratto
è dato da
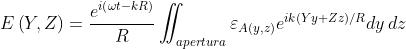
dove ora si è introdotta la possibilità che la forza della sorgente che illumina
l'apertura sia variabile. L'esponenziale che sta davanti al segno di integrale
contribuisce solo alla fase dell'onda in (Y, Z), mentre il termine 1/R che provoca
la diminuzione della ampiezza dell'onda andando dall'apertura al piano di osserva-
-zione, nella approssimazione di Fraunhofer è costante su tutto il piano stesso.
Quindi per quanto riguarda la distribuzione della ampiezza dell'onda sul piano di
osservazione, il fattore che moltiplica l'integrale è non essenziale. Se si definiscono
i parametri di frequenza spaziale come
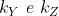
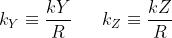
e si introduce la funzione apertura , allora per il campo diffratto si ha:
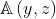
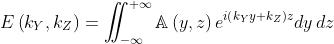
Ciò ovviamente significa che
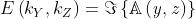
Nel caso di Fraunhofer il campo diffratto è la trasformata di Fourier della
distribuzione del campo sull'apertura espressa da .
In altre parole, ogni macchia luminosa della figura di diffrazione sta ad indicare la
presenza di una componente di data frequenza spaziale nella rappresentazione
della funzione apertura.
Questo è solo uno dei tanti esempi possibili di applicazione dei metodi di
Fourier nel campo dell’ ottica.
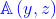

1 )
Determinare la trasformata di Fourier della funzione impulso quadrato della
sottostante figura.
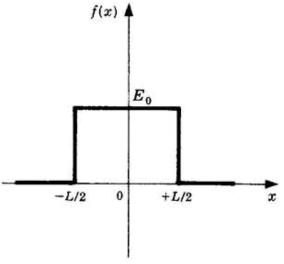
L'origine è disposta in modo da rendere la funzione pari e rendere quindi nulla la
trasformata seno.
La trasformata coseno è
o
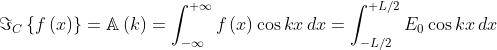
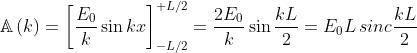
Come in un precedente problema, si ottiene una
funzione sinc, ed essa è anche l'inviluppo dello
spettro di frequenza della soprastante figura (c9).
Se si vuole conoscere quanto pesa il contributo
di una data frequenza nel determinare il valore
di f(x), basta introdurre quel valore di k nella
funzione sinc e ricavare la specifica .
Si noti che f(x) può essere messa in relazione con
la funzione apertura di una fenditura sottile e lunga,
per cui la sua trasformata riproduce la ampiezza del campo diffratto già studiata
nele precedenti pagine.
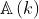

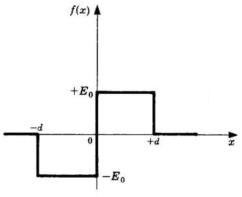
2)
Determinare e trasporre in grafico la trasformata complessa di Fourier della funzione
della seguente figura.
Dato che
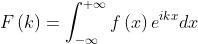
si deve determinare
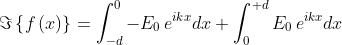
Ciò è semplicemente
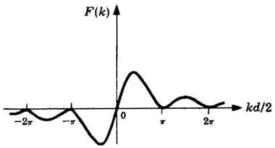
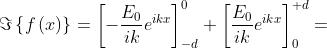
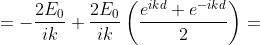
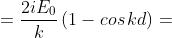
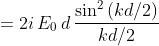
La figura a lato rappresenta il grafico della trasformata.

3)
L'impulso della sottostante figura a) può essere espresso come
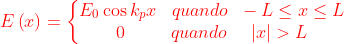
Ora, se è un impulso quadrato di ampiezza unitaria, come in figura b)
. In entrambi i casi, è la frequenza spaziale della regione
oscillatoria dell'impulso. Determinare .
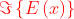
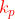
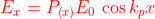
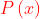
Dato che E(x) è pari :
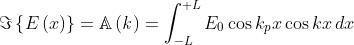
Usando la identità
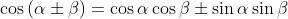
l'integrale diventa
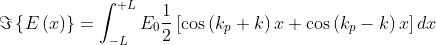
e quindi
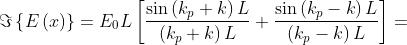
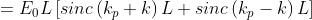
Se
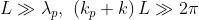
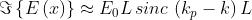

4)
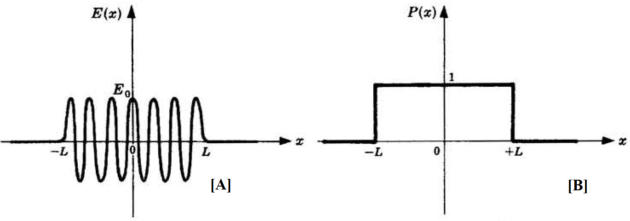
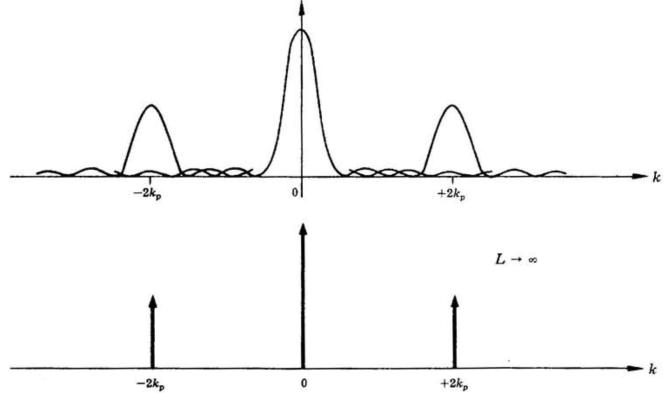
Determinare la trasformata di Fourier del treno d'onda dato da
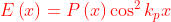
dove P(x) è l'impulso quadrato unitario della soprastante figura [B]. Tracciare un
diagramma della trasformata e del limite cui tende quando l'impulso si estende
all'infinito.
Si usa la trasformata complessa e quindi si rappresenta E(x) in forma esponenziale
come segue
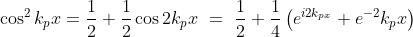
Di conseguenza,
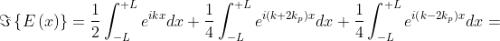
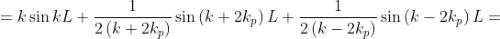
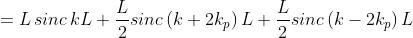
La sottostante figura dà il grafico della trasformata e del suo limite per
.
Si noti che benché si inizi il calcolo con la trasformata complessa, il risultato finale
è reale, come lo era nel precedente problema. In questo caso la funzione è pari e
.
Si tenga presente che E(x) può essere messo in relazione con una funzione
apertura (in questo caso, quella di un lungo reticolo). Quindi la sottostante figura
riproduce l'ampiezza del campo diffratto di Fraunhofer.
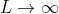
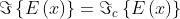

5)
Calcolare e tracciare il grafico della trasformata complessa di Fourier della funzione
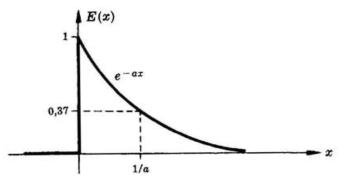
E(x) della figura a lato. Si osservi che essa
può essere espressa come
dove a è una costante positiva e U(x) è la
funzione gradino unitario eguale a zero per
x<0 e a uno per x>0.
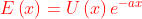
Dalla definizione della trasformata
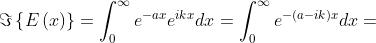
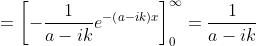
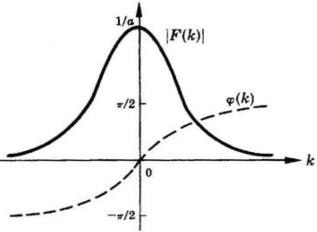
Per tracciare il grafico di questo spettro di frequenza complesso, lo si esprime
anzitutto in termini di ampiezza e di fase, come
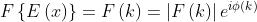
Moltiplicando sopra e sotto per , si ha
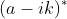
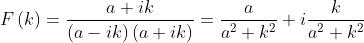
Ne segue che
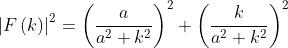
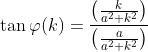
Di conseguenza
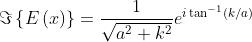
e questa è rappresentata qui graficamente

6)
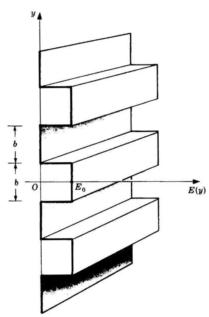
Si consideri una fenditura sottile e lunga (nella direzione delle y), coperta da una
mascherina di ampiezza per cui il campo diminuisce linearmente allontanandosi dal
centro come nella sottostante figura. Determinare il campo diffratto di Fraunhofer
nel caso di luce monocromatica incidente normalmente.
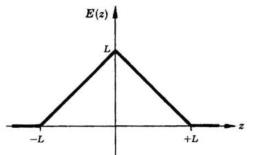
Si tratta di una funzione pari e quindi
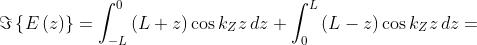
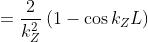
Tramite una trasformazione trigonometrica si ha
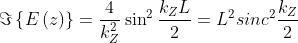
e il quadrato di questa funzione è proporzionale alla distribuzione della intensità di
radiazione. Il procedimento di applicare una mascherina ad una apertura, gene-
-ralmente per ridurre i massimi secondari di rifrazione, è noto come apodizzazione.

7)
La funzione delta di Dirac è definita come
ed è nota anche come funzione impulso unitario. Una delle sue caratteristiche
più interessanti è la proprietà di filtro
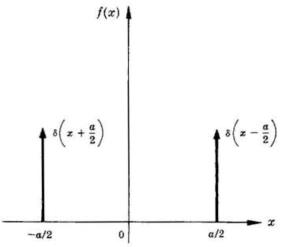
Dimostrare che . Determinare
inoltre la trasformata delle due funzioni delta
che compongono la funzione di figura a lato.
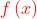
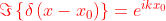
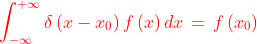

Dalla definizione della trasformata
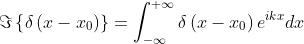
Se ora si considera come , la proprietà di filtro dice che l'integrale è eguale
a , o in questo caso a
. Quindi
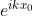
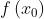
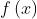
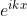
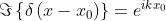
Dovrebbe risultare evidente dalla forma della trasformata che se una funzione f(x)
consiste di una somma di funzioni individuali, è a sua volta la somma
delle loro trasformate individuali. Quindi in termini generali, se
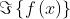
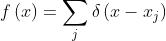
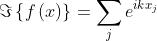
In particolare nel caso in esame
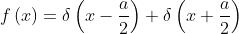
e quindi
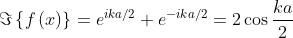
Si ricordi l'esperimento di Young. Finché esso consisteva di due fenditure di
larghezza infinitesima il campo di interferenza idealizzato era cosinusoidale.
In altre parole, se la funzione apertura corrisponde alla soprastante figura,
il sistema di distribuzione della intensità di radiazione consiste di frange propo-
-zionali al quadrato di un coseno.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





