A volte un urlo è meglio di una tesi

OTTICA TEORICA

DIFFRAZIONE DI FRESNEL - SISTEMI CIRCOLARI

Occorre ora affinare un po' la semplice teoria di Huygens-Fresnel, il che non era necessario finché si trattava di angoli piccoli su campi lontani. Si consideri il fatto che se le onde secondarie fossero davvero sfericamente simmetriche, un fronte d'onda primario genere- -rebbe due perturbazioni, una che si propagherebbe in avanti e una all'indietro: e ciò ovviamente non avviene. La soluzione del dilemma, formulata da Fresnel, consiste nell'assumere che la ampiezza delle onde secondarie diminuisca man mano che ci si allontana dalla direzione di propaga- -zione della onda primaria. Nel limite di Fraunhofer dei paragrafi precedenti ogni onda secondaria contribuiva principalmente nella direzione in avanti, e quindi questa difficoltà poteva essere trascurata. Ora invece si deve moltiplicare la ampiezza di ogni onda sferica secondaria per un fattore di obliquità o di inclinazione, che risulta avere la forma

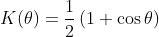
come illustrato in figura [1]

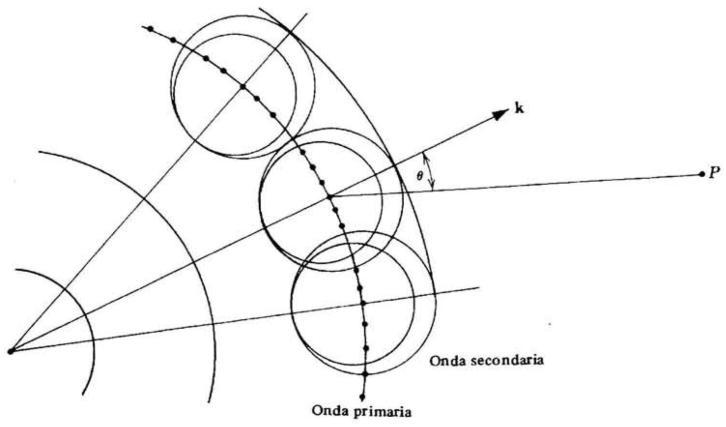
[Fig. 1]

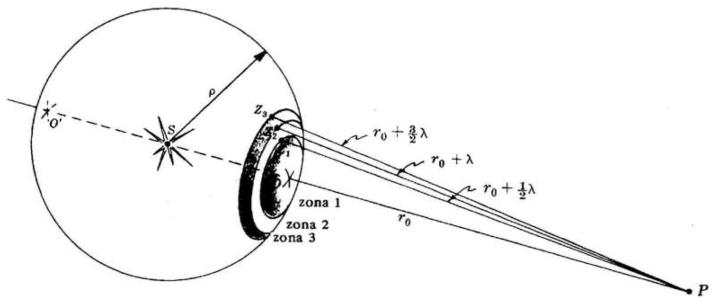
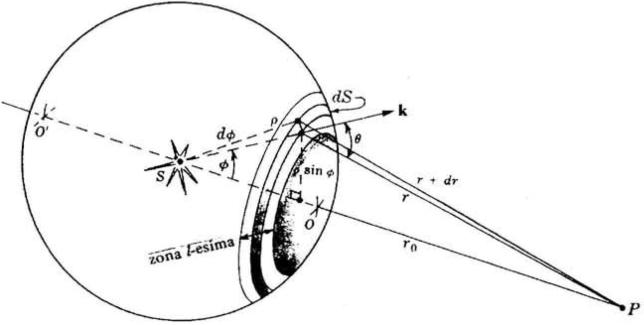
Si consideri in figura [2] l'onda emessa da S nel caso non vi siano ostacoli di sorta. Ogni elemento di superficie dS del fronte d'onda sferico primario di raggio p emette onde secondarie di forma

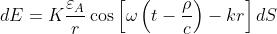
Il fronte d'onda primario viene suddiviso in zone anulari note come zone di Fresnel o zone di mezzo periodo. Integrando dE sulla zona l-esima (l = 1,2,3, ... ) (figura [3]) si trova che il suo contributo al campo nel punto P è

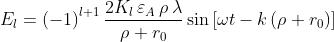
figura [2]

figura [3]

Il segno del contributo sarà positivo o negativo a seconda che l sia dispari o pari; ciò significa che i contributi di zone adiacenti sono sfasati tra di loro e tendono ad annullarsi a vicenda. L'annullamento però non può essere completo dato che il fattore di obliquità indebolisce il contributo delle zone successive. Sommando le ampiezze dei campi relativi a tutte le m zone,

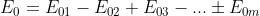
e supponendo che zone adiacenti abbiano ampiezze quasi eguali, dato che K varia lentamente con m, si può dimostrare che

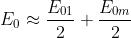
quando m è dispari, e

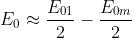
quando m è pari.

In entrambi i casi, il contributo della zona m-esima, che circonda O', si annulla dato che . Quindi

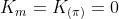
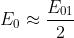
cioè la perturbazione ottica prodotta in P dalla intera onda nel caso non vi siano ostruzioni di sorta è pressappoco eguale a metà del contributo della sola prima zona. Si pensi ora di dividere la prima zona in N zone minori distinte caratterizzate dalle rispettive distanze da P:

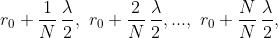
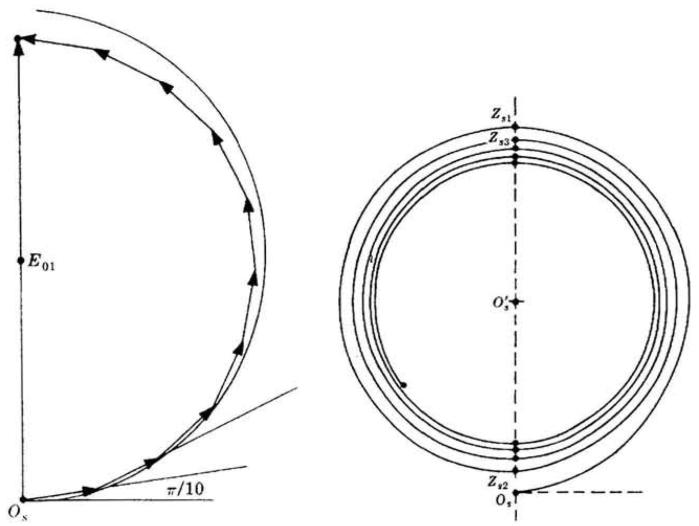
figura [5]

figura [4]

I contributi di ognuna di queste sotto zone al campo possono essere sommati vettorialmente come nel diagramma fasoriale di figura [4], dove N=10. Il fattore di obliquità determina una leggera diminuzione graduale delle ampiezze costituenti, che quindi si combinano a formare una specie di spirale. Se si arriva ad una spirale circolare e stretta nota come curva di vibrazione (figura [5]), che compie mezzo giro alla aggiunta di ogni nuova zona. Si noti che i punti , (vedi figura [2]) del fronte d'onda corrispondono ai punti della curva, le cui spire girano e infine terminano in . La ampiezza del campo dell'onda in assenza di ostacoli, è eguale alla lunghezza del vettore che va da . Analogamente, il vettore compreso tra dà il contributo della prima zona, , ed è evidente che . Si supponga ora, riferendosi alla figura [2], di inserire in O uno schermo opaco munito di un foro circolare di raggio R e perpendicolare a . Nel sottostante problema 1) si dimostra che l'area di ogni singola zona è con buona approssimazione eguale a

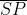
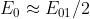
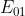
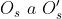
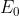
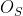
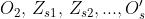
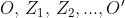
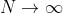
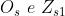
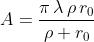
e quindi il numero di zone m che da P sono viste interne al foro sono approssimativa- -mente

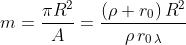
Se m è un numero intero pari,

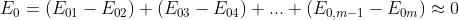
e in P si ha una macchia scura. Se invece m è un intero dispari,

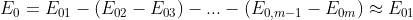
che corrisponde ad una macchia luminosa. In entrambi i casi, m è relativamente piccolo in confronto al numero di zone dell'onda senza ostruzioni e . La curva di vibrazione mette bene in luce l'effetto, dato che il campo per la prima zona cor- risponde a ,mentre quello relativo alle prime due zone è solo . Ovviamente può darsi che l'apertura lasci scoperta solo parzialmente una zona, in questo caso in P si avrebbe una macchia grigia. Considerazioni analoghe valgono anche per punti non situati sull'asse e, per simmetria, la figura di diffrazione su un piano passante per P risulta costituita da una serie di anelli concentrici di densità di flusso variabile.

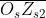
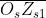
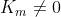
Se nel punto O di figura [2] invece di un foro si colloca un disco o una sfera opachi e piccoli, questi ostruirebbero le prime l zone per cui

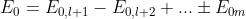
Come nel caso di onda che si propaga senza ostacoli, m è molto grande, e . Il disco può coprire solo una porzione della l-esima zona, ma in ogni caso si ha una macchia luminosa in ogni punto dell'asse, salvo in quelli immediatamente dietro all'ostacolo. In altre parole, esattamente al centro dell'ombra, si ha una zona illuminata, detta macchia di Poisson dal nome del celebre scienziato francese che si ostinò a sostenere che un tale risultato era assurdo. Come nel caso della curva di vibrazione, la periferia dell' ostacolo corrisponderà a un punto , della spirale. La lunghezza corrisponde al campo nel punto P dell'asse e evidentemente è non nullo dovunque si trovi .

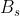
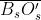
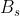
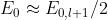
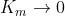
1 ) Riferirsi alla soprastante figura [3] per ricavare una espressione dell'area della l-esima zona di Fresnel di un fronte d'onda sferico. Dimostrare che il rapporto tra questa area e la sua distanza media da P è indipendente da l, eguale cioè per tutte le zone. Discutere il significato fisico del fatto.

L'elemento di superficie può essere espresso come

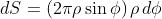
da cui si ha che l'area della calotta sferica è

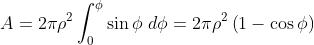
Per la legge dei coseni applicata alla zona l-esima

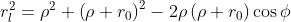
per cui

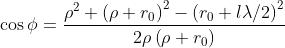
L'area della zona l-esima è l'area della calotta sferica fonnata dalle prime l zone,

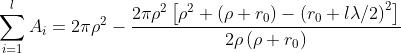
meno l'area della calotta formata dalle prime l-1 zone,

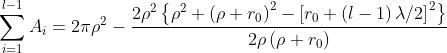
Quindi

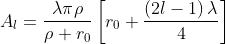
Il secondo termine può essere in generale trascurato, ottenendo così una espressione indipendente da l, il che sta a significare che le zone hanno appros- -simativamente tutte la stessa area. La distanza media tra la zona l-esima e P è indicata con . Le distanze tra P e i bordi della zona sono , per cui

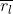
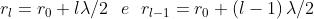
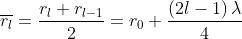
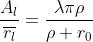
Ne segue che

che è sicuramente indipendente da l. Ci si può quindi aspettare che il contributo dato dalla zona l-esima alla ampiezza del campo dipenda da e che quindi sia indipendente da l, come in realtà succede.

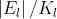
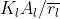
2) Ricavare una espressione per l'area della l-esima zona di Fresnel come la si vede dal punto P, nel caso in cui le onde incidenti siano piane. Calcolare l'area della prima zona quando e il punto di osservazione è a 0,5 rn dal fronte d'onda. Che errore si commette se si trascura nell'espressione dell'area il termine in ?

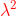
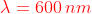
Dal precedente problema

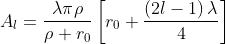
per un fronte d'onda sferico di raggio . Nel caso in esame le onde sono piane, cioè . . Quindi e

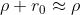
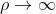
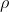
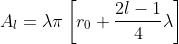
In particolare quando

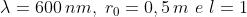
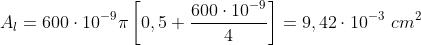
Il valore approssimato dell'area, trascurando il secondo termine, è

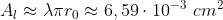
La differenza tra i due è cioè circa lo 0,00003%

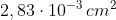
3) Ricavare una espressione per il raggio esterno della l-esima zona di Fresnel di un fronte d'onda piano vista da un punto a distanza .

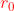
Dalla sottostante figura, la distanza tra P e la periferia della zona l-esima è evidentemente

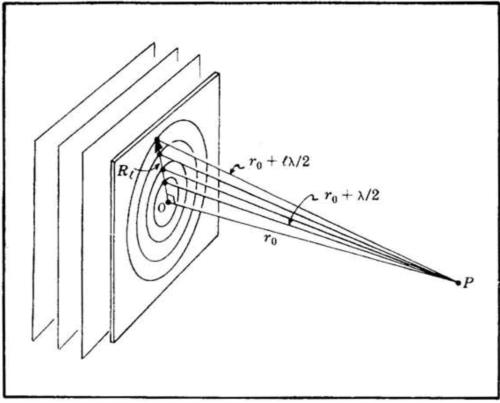
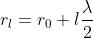
Ne segue,

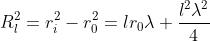
In generale l'ultimo termine è trascurabile e si assume per , il valore

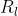
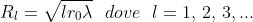
4) Un raggio proveniente da un laser a He-Ne viene espanso e collimato inviandolo nella estremità posteriore di un telescopio focalizzato all'infinito. Calcolare il valore esatto e approssimato del raggio della prima zona di mezzo periodo nel caso che l'onda sia osservata assialmente da 1,58 m di distanza.

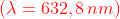
Il valore approssimato del raggio è dato dal precedente problema, come

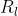
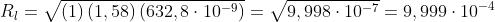
O, se si preferisce, = 1 mm. Più esattamente,

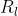
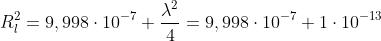
5) Un foro di 3 mm di diametro praticato in uno schermo opaco è illuminato normalmente da onde piane di lunghezza 550 nm. Una piccola sonda viene spostata lungo l'asse centrale per rilevare la densità di flusso. Determinare le posizioni dei primi tre massimi e minimi.

I massimi si hanno quando il foro scopre un numero dispari di zone. Quindi, essendo

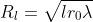
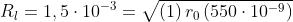
che porta a

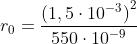
e alla distanza di solo la prima zona è scoperta, per cui si ha un massimo. Il massimo successivo si ha quando il foro scopre tre zone, cioè per

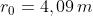
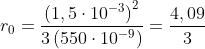
e . Risulta evidente che i massimi successivi cadono a 0,82,0,58 e 0,45 m di distanza. Analogamente, i minimi corrispondono ad un numero pari di zone scoperte e quindi basta dividere 4,09 m per 2, 4, 6, ... per determinare la loro posizione. Così il primo minimo si ha a 2,05 m.

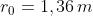
6) Onde piane colpiscono normalmente un foro circolare di 2,09 mm di raggio. Uno schermo posto a 1 m dal foro intercetta la figura di diffrazione. Descrivere la figura di diffrazione nel punto centrale .

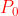
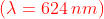
Anzitutto si determina il numero delle zone di Fresnel scoperte dalla apertura di raggio R. L'area di ogni singola zona, per il soprastante problema 2), è

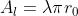
mentre l'area del foro è . Per cui il numero N delle zone è

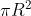
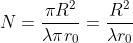
Nel caso specifico

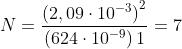
e nel punto centrale si ha una macchia luminosa.

7) Si considerino ancora delle onde piane che colpiscono perpendicolarmente un foro circolare. Se da un dato punto P dell'asse il foro scopre 1/4 della prima zona di Fresnel, qual’è il valore della intensità di radiazione in P in funzione di , la intensità che si ha in P quando non vi sono ostruzioni?

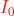
In figura a lato è riportata la curva di vibrazione. Si tenga presente che nella realtà la spirale è avvolta molto stretta, per cui in una regione abbastanza piccola essa può essere assimilata ad un cerchio. La corda corrisponde alla ampiezza cercata, con posto ad un quarto della lunghezza dell'arco tra e cioè un quarto della prima zona. Evidentemente

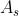
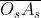
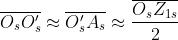
e quindi

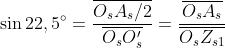
dove sin 22,5° = 0,383. Ma questo è il rapporto tra le ampiezze dei campi; il suo quadrato è quindi il rapporto tra le intensità di radiazione richiesto. Ricordando che è eguale al doppio della ampiezza che si ha

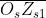
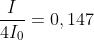
e quindi . Si tenga presente che è anche la intensità di radiazione incidente, dato che le onde sono piane.

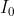
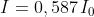
8) Una onda monocromatica piana colpisce normalmente uno schermo opaco che contiene una apertura a forma di anello circolare di raggio 1,000 mm e 1,414 mm. Determinare la ampiezza del campo elettrico in un punto dell'asse distante 2,222 m in funzione della ampiezza del campo elettrico incidente . Un foro di raggio 1,414 mrn contiene N zone con

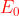
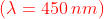
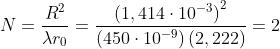
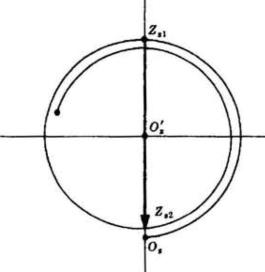
Analogamente un disco di raggio 1 mm esclude solo la prima zona - quindi solo la seconda contribuisce al campo. La ampiezza del campo risultante è mostrata nella figura a lato.

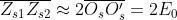
Si noti che i due vettori sono diretti in verso opposto, sono cioè sfasati di radianti.

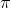
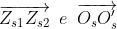
9) Delle onde piane colpiscono perpendicolarmente con intensità di radiazione uno schermo opaco dove è praticata la apertura indicata nella sottostante figura. Determinare la intensità di radiazione in un punto dell'asse a 4 m di distanza dallo schermo.

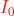
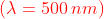
In tutti i problemi di aperture il primo passo consiste nella determinazione del numero delle zone che contribuiscono al campo. Per un foro di raggio 2 mm

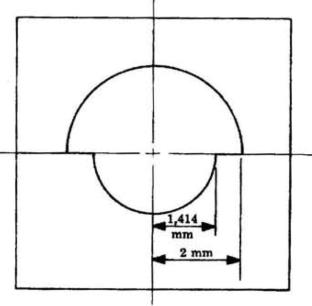
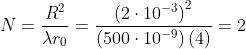
mentre per R = 1,414 mm, N = 1. Evidentemente si tratta in questo caso di dete- -rminare il campo risultante dal contributo della prima e di metà della seconda zona. E' un caso diverso da quello di un unico foro circolare che scopre una zona e mezzo a partire dalla prima. In quest'ultimo caso, se un punto B si trovasse sulla periferia della apertura, allora il punto associato sarebbe , tre quarti di un giro della spirale e il campo corrispondente sarebbe quindi . Si pensi invece di dividere la seconda zona, una parte della quale è vista dalla apertura, ad esempio, in dieci sottozone nel modo indicato nella sopra- -stante figura [3]. I campi dovuti alle dieci sottozone anulari si sommano a dare una risultante equivalente a mezzo giro della spirale. Nel caso in esame si devono sommare i dieci segmenti di queste sottozone scoperte dalla parte esterna della apertura. Ognuno di questi vettori campo è lungo la metà della lunghezza del caso precedente e quindi si ottiene una spirale come nel caso precedente ma ora ridotta a metà grandezza. Invece del contributo di per la intera seconda zona, si ottiene il contributo di metà della zona.

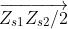
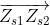
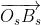
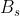
Il valore completo del campo è quindi dato dalla somma vettoriale.

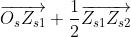
e la sua ampiezza in funzione della ampiezza del campo incidente è

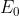
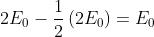
La intensità di radiazione in P è quindi eguale alla intensità incidente .

Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara

Math.php-c