



La vita non è fatta dai desideri bensì dagli atti di ciascuno
OTTICA TEORICA
APERTURE RETTANGOLARI E CIRCOLARI
APERTURE RETTANGOLARI E CIRCOLARI - DIFFRAZIONE DI FRAUNHOFER
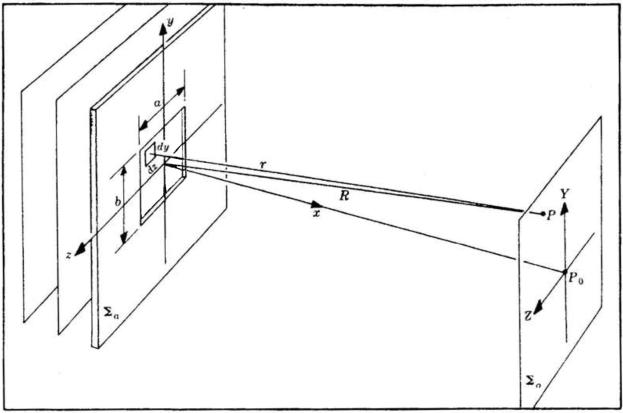
La figura di diffrazione su campo lontano associata ad una apertura rettangolare può
essere determinata riferendosi alla sottostante figura. Ogni porzione elementare di area
agisce da sorgente monocromatica puntiforme di onde secondarie di Huygens
la cui rappresentazione complessa è
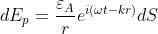
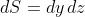
dove con si indica la forza della sorgente per unità di superficie. La condizione di
Fraunhofer porta a sostituire alla espressione esatta di r
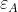
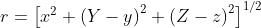
mentre l’epressione approssimata
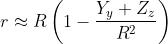
Di conseguenza il valore complessivo del campo nel punto P diventa
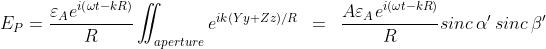
dove A è l'area dell'apertura, . Dato che ,
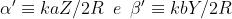
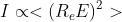
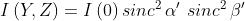
un risultato che si poteva prevedere sulla base dello studio già fatto della diffrazione
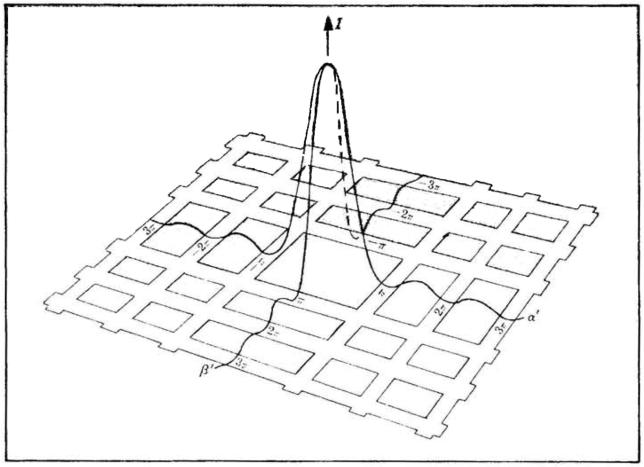
nel caso di una singola fenditura. La sottostante figura, illustra la distribuzione della
intensità di radiazione in funzione di , o di Z ed Y, il che è equivalente
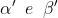
La forza della sorgente per unità di superficie delle emittenti puntiformi,
è a sua
volta legata al valore del campo elettrico dell'onda primaria incidente dalla relazione
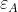
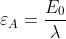
dove è la ampiezza del campo primario sopra l'apertura.
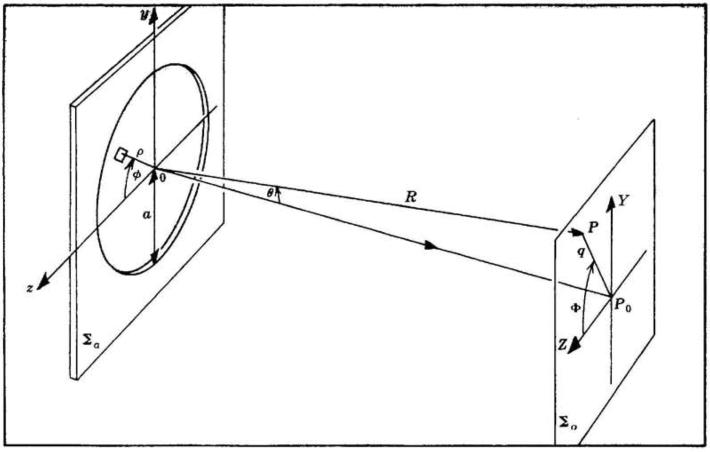
La espressione sopra ricavata di come integrale doppio è un 'espressione
generale e può essere applicata anche nel caso di apertura circolare come quella
illustrata nella sottostante figura. Dopo alcuni passaggi analitici piuttosto complicati
in coordinate polari si trova che la distribuzione della intensità di radiazione è data da
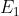

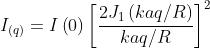
è una funzione di Bessel del primo ordine definita dalla serie
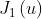
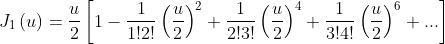
Essa assomiglia vagamente ad una onda seno smorzata. Dato che ,
la densità di flusso può essere espressa anche come
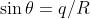
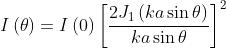
Si tratta della famosa figura di Airy, cosiddetta dal nome del celebre astronomo
britannico che per primo ricavò questa formula.
Essa consiste di un disco centrale luminoso circondato da un sistema di anelli concentrici
alternativamente scuri e luminosi. Come illustrato nella sottostante figura, il primo zero
si ha per , e se si indica con la distanza tra e questo zero esso
può essere considerato come il raggio del disco di Airy, cioè
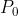
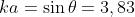
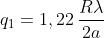
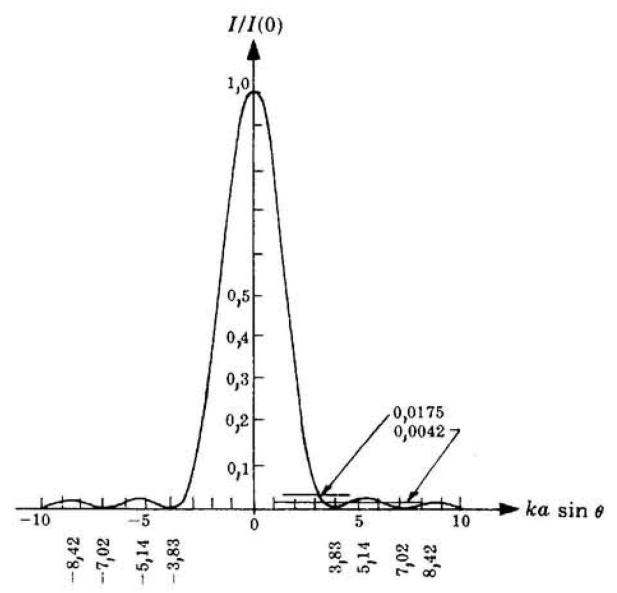
La discussione in questione ha una grande importanza pratica dato che l'immagine
di una sorgente puntiforme prodotta da un sistema ottico ideale formato da lenti o
specchi circolari non è un punto, ma piuttosto una figura di Airy

1 )
Dimostrare che una apertura rettangolare orizzontale genera una figura di
diffrazione di Fraunhofer che ha al suo centro una zona luminosa rettangolare
verticale. Che effetto ha sulla dimensione del sistema di frange l'aumento del
valore della lunghezza d'onda?
[a]
Il massimo centrale è limitato da quattro segmenti di retta nodali lungo i quali I= O;
ciò si verifica per , come in figura [a]. Di conseguenza le
metà dei lati del massimo centrale, , soddisfano alle equazioni
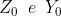
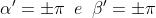
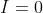
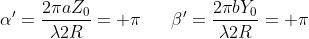
oppure
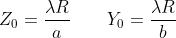
Per una-apertura orizzontale
e quindi cioè la regione rettangolare
luminosa è verticale.
Quando
cresce, crescono sia Zo che Yo e l'intera figura assume dimensioni
maggiori. Analogo effetto si ha se cresce R.
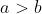
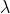
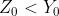

2)
Determinare, almeno approssimativamente, le intensità di radiazione relative dei
quattro massimi secondari diagonali più vicini al massimo centrale in una figura di
Fraunhofer prodotta da una apertura rettangolare. Che relazione c'è tra questi e
il sesto massimo secondario assiale?
Assumendo anche in questo caso che i massimi cadano a metà strada tra minimi
consecutivi, i massimi in questione si hanno per
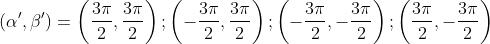
Il problema chiede però di valutare
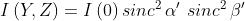
in questi punti ed a tal fine conviene usare la approssimazione sviluppata in un
precedente problema. Di conseguenza con m=1
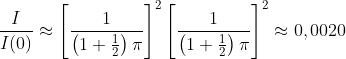
per ognuno dei primi massimi diagonali. Il sesto massimo sui quattro assi si ha
rispettivamente per
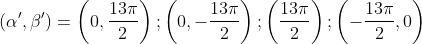
Il valore della intensità di radiazione relativa è eguale per tutti e quattro ed eguale a
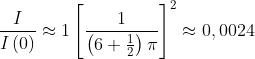
Risulta che le macchie luminose poste lungo gli assi coordinati sono notevolmente
più pronunciate di quelle fuori dagli assi. Gli spigoli dell'apertura in effetti produ-
-cono nella immagine di diffrazione lunghe strisce luminose perpendicolari

3)
Un buco rettangolare orizzontale di 0,25 mm x 0,75 mm in uno schermo opaco è
illuminato normalmente da onde piane di luce azzurra prodotta da un laser a ioni
di argo con
. La immagine di diffrazione viene raccolta su uno schermo
posto nel piano focale di una lente positiva vicina .
Descrivere il massimo centrale che ne risulta.
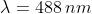
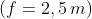
Come nel problema 1), la regione rettangolare centrale della figura è limitata dalle
prime rette a intensità di radiazione nulla, per cui

In questo caso per cui
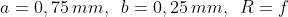
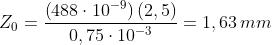
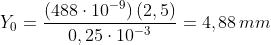
La regione centrale è un rettangolo verticale 9,76 mm x 3,26 mm

4)
Una onda piana monocromatica di
= 500 nm colpisce normalmente una apertura
rettangolare orizzontale di 1 mm x 5 mm praticata in uno schermo opaco. Al centro
dell'apertura è disposto un rettangolo opaco orizzontale di 0,1 mm x 0,5 mm.
Descrivere la distribuzione della intensità di radiazione che si ha sul piano focale di
una lente convergente vicina avente distanza focale di 1 m
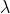
Si parte dalla considerazione che la apertura di 1 mm x 5 mm se non ci fosse alcuna
ostruzione darebbe in P un campo . Si può inoltre supporre che il rettangolo di
0.1 mm x 0,5 mm oscuri un sistema di emittenti di Huygens-Fresnel che in caso
contrario produrrebbero un campo di valore . Il campo esistente realmente in
P è allora
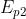
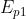
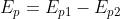
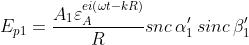
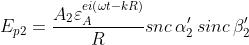
dove
I termini sono le aree delle aperture corrispondenti. Quindi
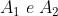
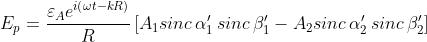
e la densità di flusso è
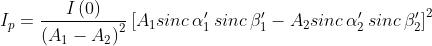
dove corrisponde a Nel caso particolare in esame

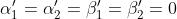
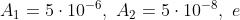
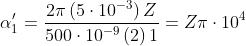
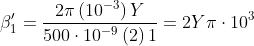
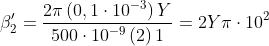
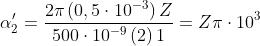

5)
Ricavare una stima approssimata della estensione del disco di Airy nello spettro
del visibile per una lente, in funzione del suo numero f (rapporto tra la distanza
focale e il diametro).
Partendo dal raggio del disco di Airy,
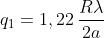
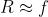
si sfrutta anzitutto il fatto che cioè
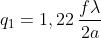
Allora, essendo , il diametro della lente, il diametro del disco è
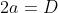
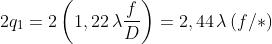
dove f/* è il numero f. Nel campo del visibile si può approssimativamente assumere
eguale a 1000 nm. Quindi in milionesimi di metro o micron.
Una lente di macchina fotografica,con
f/* eguale a 1,4, forma sul piano della pellicola una immagine di un punto lontano
di diametro
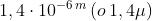
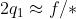
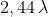

6)
Un raggio di luce monocromatica collimata (
= 600 nm) colpisce normalmente
una lente convergente di 1,2 cm di diametro e 50 cm di distanza focale.
Determinare le dimensioni angolari e lineari del disco centrale della figura di dif-
-frazione che compare sul piano focale.
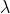
Il disco di Airy ha un raggio di
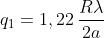
dove ora , e quindi il suo diametro è
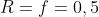
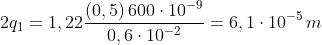
Il "raggio angolare" è solitamente indicato come
, dove . Ne segue
che il diametro angolare del disco è
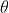
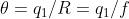
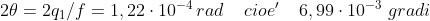

7)
Il telescopio a rifrazione secondo per grandezza in tutto il mondo è quello del Lick
Observatory di 36 pollici e 56 piedi (~17 m) di distanza focale. Calcolare il raggio
del secondo anello luminoso della figura di Airy di una stella che si forma sul piano
focale dell'obiettivo.
[b]
Dalla soprastant figura [b], si vede che il secondo massimo secondario si ha per
. Quindi
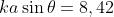

e con R=f e una lunghezza d'onda media di 550 nm,
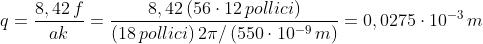

8)
Applicare il criterio di Rayleigh formulato in un precedente problema, al caso di una
apertura circolare e ricavare una espressione per , la distanza angolare
minima risolubile tra due oggetti puntiformi lontani.
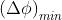
In base al principio di Rayleigh, due sistemi di Airy incominciano ad essere risolubili
quando il massimo centrale di uno coincide con il primo minimo dell'altro. Ma ciò
corrisponde ad una distanza eguale al raggio angolare del disco di Airy, e quindi
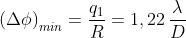
dove D è il diametro dell'apertura

9)
Determinare la distanza angolare minima intercorrente tra due stelle di eguale
luminosità che può essere risolta (secondo il criterio di Rayleigh) dal telescopio
Hale da 200 pollici del Monte Palomar. Che distanza lineare si ha se la distanza
focale principale è di 666 pollici (~ 17 m)?
In base al precedente problema e assumendo
= 550 nm
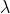
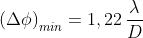
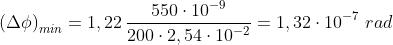
o 0,027 secondi di arco (da confrontare, ad esempio, con i 18 secondi del diametro
angolare massimo di Marte visto dalla Terra). La distanza lineare corrispondente
nella immagine piana o limite di risolubilità, è
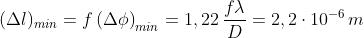


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





