Ho il cratere che non funziona. (catetere)

OTTICA TEORICA

EQUAZIONI DI MAXWELL E ONDE ELETTROMAGNETICHE

EQUAZIONI DI MAXWELL E ONDE ELETTROMAGNETICHE Nel 1865 Maxwell unificò ed estese le leggi di Faraday, di Gauss e di Ampère definendo un gruppo di equazioni comprensive note da allora come equazioni di Maxwell. Esse stabiliscono una relazione tra le variazioni temporali e spaziali della intensità del campo elettrico E e della induzione magnetica B. Nello spazio libero e usando coordinate cartesiane, le equazioni di Maxwell possono essere scritte in forma differenziale nel modo seguente:

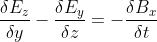
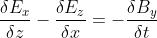
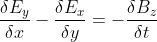
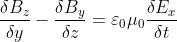
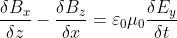
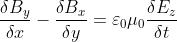
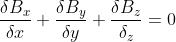
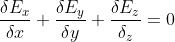
In queste equazioni, le proprietà elettriche e magnetiche del mezzo, in questo caso il vuoto, sono rappresentate dalle costanti e la permettività e la permeabilità rispettivamente. Manipolando queste espressioni, Maxwell riuscì a dimostrare che tutte le componenti del campo elettrico e del campo magnetico obbediscono alla equazione differenziale delle onde in forma esplicita

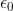
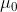
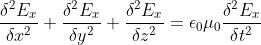
mentre analoghe .relazioni valgono per . Ne segue che campo elettrico e campo magnetico si accoppiano a formare un'onda elettromagnetica che si propaga nello spazio alla velocità .Maxwell, introducendo i valori numerici di e calcolò che in buon accordo col valore della velocità della luce misurato sperimentalmente da Fizeau. La conclusione era inevitabile: la luce era un'onda elettroma- -gnetica. Il simbolo usato generalmente per indicare la velocità della luce nel vuoto è c, e il valore attualmente accettato per essa è

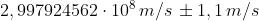
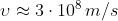
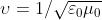
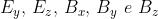
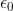
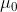
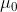
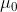
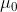
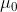
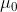
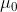
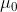
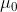
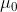
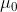
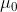
1) Una onda elettromagnetica piana è un'onda i cui campi elettrico e magnetico sono costanti in un piano perpendicolare alla direzione di propagazione. Dimostrare che una onda del genere deve avere il campo elettrico trasversale rispetto alla direzione di propagazione.

Se l'onda si propaga nella direzione dell'asse z, il campo elettrico deve essere indipendente da x e da y ,deve cioè essere . L'ultima equazione di Maxwell

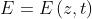
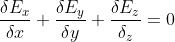
diventa quindi

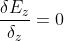
dato che E non è funzione né di x né di y . L'equazione viene quindi a dire che Ez = costante e quindi che non presenta alcun interesse quanto all'onda elettromagnetica, la quale deve invece variare lungo z. L'onda può quindi avere solo componenti secondo gli assi x e y e quindi E è trasversale.

2) Si supponga di avere una onda elettromagnetica piana polarizzata linearmente il cui campo elettrico abbia la forma E = Ex(z, t) j. Dimostrare che B = By(z, t) j.

Il campo elettrico è polarìzzato lungo l'asse x, come risulta dalla presenza del solo termine in j. Inoltre l'onda si propaga nella direzione delle Z. Dato che Ey = Ez = 0 e Ex = Ex(z,t), le prime tre equazioni di Maxwell si riducono a

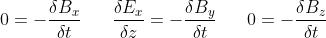
Ciò significa che Bx e Bz sono costanti rispetto al tempo e quindi non ci interessano. By è l'unico termine che varia nel tempo e quindi B = By(z,t)j è la componente magnetica dell'onda. Si noti che E e B sono normali tra di loro e anche alla direzione di propagazione ..

3) Data un'onda elettromagnetica piana armonica il cui campo E abbia la forma determinare il corrispondente campo B e tracciare un diagramma dell'onda

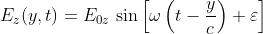
Essendo Ex = Ey = 0, la prima equazione di Maxwell diventa

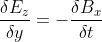
oppure

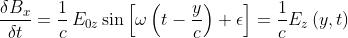
l campi elettrico e magnetico sono ortogonali, i relativi valori sono legati dalla relazione E=cB, ed entrambi sono normali alla direzione di propagazione.

4) In termini molto generalì, un'onda elettromagnetica si propaga nella direzione data dal prodotto vettoriale* E x B. Dimostrare che ciò è vero per un'onda piana armonica che si propaga nella direzione delle x positive e il cui campo elettrico sia E(x, t) = Ez(x, t).

* Qui e nel seguito verranno adottate le notazioni a x b per indicare il prodotto vettoriale e a • b per il prodotto scalare in uso nei testi in lingua inglese.

Dalle prime tre equazioni di Maxwell si ricava

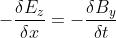
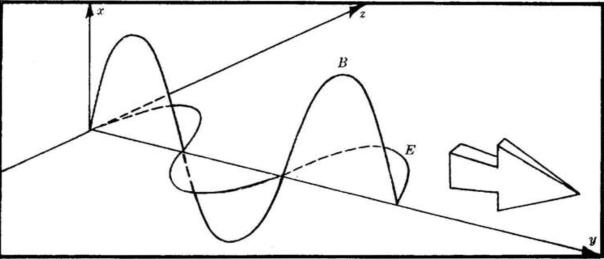
dove Ex = Ey = 0. Da qui, integrando, si ha . I campi E e B sono sfasati. In forma vettoriale si ha Dato che ,tutto quadra.

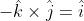
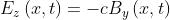
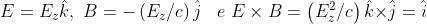
5) Si abbia un'onda elettromagnetica piana nel vuoto il cui campo elettrico (in unità SI) sia Determinare velocità, frequenza, lunghezza d'onda, periodo, fase iniziale, ampiezza del campo E e polarizzazione.

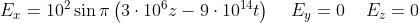
La funzione d'onda ha la forma-base

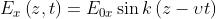
Ne segue che essa può essere scritta nella forma

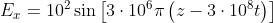
da cui si vede che e

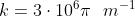
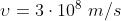
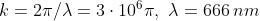
Dato che

Inoltre

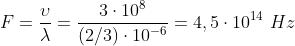
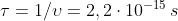
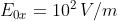
Il periodo è , mentre la fase iniziale è evidentemente nulla. L'ampiezza del campo è L'onda è polarizzata linearmente nella direzione delle x e si propaga lungo l'asse z. Quest'onda corrisponde a luce rossa

6) Scrivere un'espressione del campo magnetico associato all'onda del precedente problema.

L'onda si propaga nella direzione delle z mentre il campo elettrico E oscilla lungo l'asse x. In altre parole il campo E giace nel piano xz. Ne segue che B, dovendo essere perpendicolare sia al campo E che alla direzione di propagazione, giace nel piano yz. Quindi . Come visto in un precedente problema , quindi

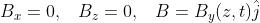
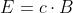
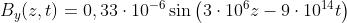
In questo caso la cui unità è il tesla (T), dove

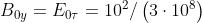
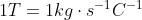
7) Un'onda elettromagnetica piana armonica di frequenza (luce verde) si propaga nel vuoto nella direzione delle x positive ed ha un campo elettrico la cui ampiezza è 42,42 V/m. L'onda è polarizzata linearmente e il piano di vibrazione del campo elettrico forma un angolo di 45° col piano xz. Scrivere delle espressioni per E e B

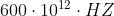
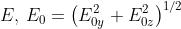
L’ampiezza del campo ,mentre, stante la polarizzazione a 45°,

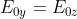
. Quindi e Scrivendo la fase nella forma , il campo elettrico diventa

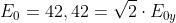
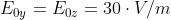
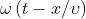
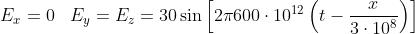
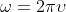
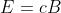
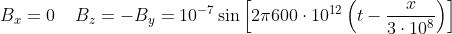
dove, ovviamente Dato che

Si noti che è perpendicolare a , come lo è a .

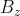
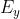
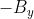
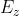
Lorem Ipsum Dolor

Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.

Add your one line caption using the Image tab of the Web Properties dialog

Made with Xara