



C'erano tanti carabinieri: avranno fatto un'arretrata
OTTICA TEORICA

RAPPRESENTAZIONE TRAMITE NUMERI COMPLESSI

LA RAPPRESENTAZIONE TRAMITE NUMERI COMPLESSI
Le espressioni trigonometriche con cui avremo a che fare possono essere notevolmente
semplificate usando gli esponenziali complessi. Si ricordi che un numero complesso z ha la
forma dove ed x e y, sono rispettivamente la parte reale e la parte
immaginaria di z. Si notì' che sia x che y sono numeri
reali. Il numero z può essere scritto anche nella
forma
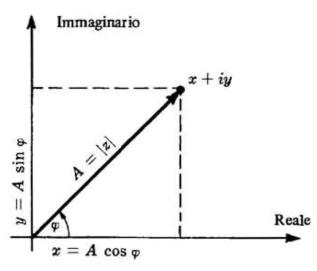
sfruttando il fatto che , come
risulta immediatamente considerando il diagramma di
Argand di figura. La formula di Eulero
permette allora discrivere
dove A è il modulo e
la fase della grandezza
complessa z. Il complesso coniugato
si ottiene
cambiando il segno davanti a j dovunque esso compare in z. Quindi
e quindi il modulo di z è semplicemente

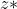
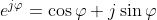
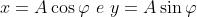
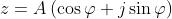
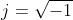
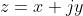
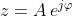
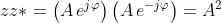
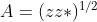
La moltiplicazione dei numeri complessi diventa particolarmente semplice quando sono
espressi in forma esponenziale. Il prodotto di
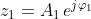
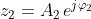
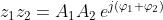
e
è semplicemente
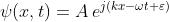
Si noti che se si scrive
la parte reale è e la parte immaginaria è dove, naturalmente,
Ne segue che in ogni calcolo si pessono usare gli esponenziali e passare alla fine
alla forma coseno o seno dell'onda prendendo la parte reale o la parte immaginaria della
risposta ottenuta.
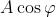
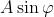
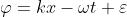

1)
Dimostrare che la parte reale del numero complesso z è data da
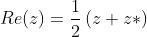
Dato che , si può scrivere
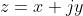
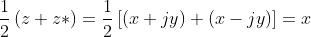
che è proprio la parte reale di z

2) Dedurre le espressioni
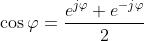
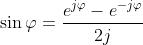
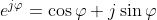
dalla formula di Eulero
Si sostituisca nella formula di Eulero , ottenendo
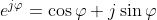
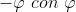
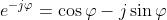
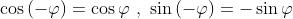
dato che . Sommando queste due espressioni si ha
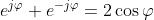
mentre sottraendole si ha
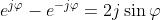
La prima formula è equivalente a quella del problema (1; la seconda a
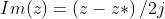

3) Scrivendo la funzione d'onda come , dimostrare che non cambia se si
aumenta o diminuisce la sua fase di
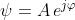
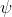
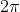
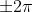
Quando si varia la fase di , la funzione d'onda assume il valore
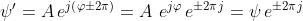
Ma per la formula di Eulero
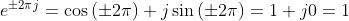
Quindi
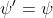

4) Dimostrare che moltiplicare una funzione d'onda complessa per ±j equivale a far
slittare la sua fase di .
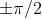
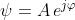
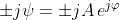
Se , allora .Ma per la formula di Eulero
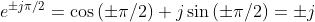
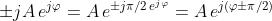
e quindi

5) Si supponga di avere due onde di ampiezza, velocità e frequenza eguali, che in una
data regione dello spazio si sovrappongono producendo la perturbazione risultante
Usando gli esponenziali complessi dimostrare che
Questa è detta onda stazionaria.
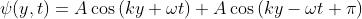
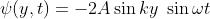
Tenendo presente che siamo interessati solo alla parte reale, si può riscrivere la
funzione d'onda come
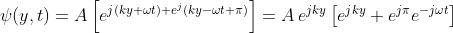
ora, per la formula di Eulero
quindi
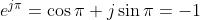
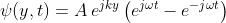
Dalla seconda formula ottenuta nel problema 2) segue che
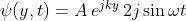
e quindi
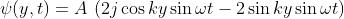
La parte reale di questa funzione d'onda è
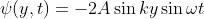
Se si fosse partiti da onde espresse in forma seno, cioè
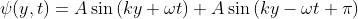
il procedimento sarebbe stato lo stesso fino all'ultimo passaggio, dove questa volta
si sarebbe assunta la parte immaginaria ottenendo
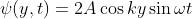
Si può indicare esplicitamente l'uso della parte reale (Re) o della parte immaginaria (Im)
scrivendo, ad esempio,
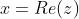
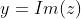


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





