



Essere maturi significa affrontare, e non evadere, ogni nuova crisi che arriva
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!
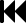

Massa
kilogrammo
kg
ESERCIZI DI VERIFICA SUI FENOMENI TRANSITORI


Esercizio 1 :
Un condensatore di capacità C = 100 μF viene caricato da 0
a 100 V mediante un circuito con costante di tempo 20 ms.
Calcolare: la carica e l’energia finali; la resistenza del circuito
di carica; la tensione V1 all’istante t1= 40 ms; il tempo t2
dopo il quale la tensione vale 80V.
[Risultati: Qf = 10 mC; Wf= 0,5 J; R = 200 Ω; Ω
V1= 86,5 V; t2= 32,2 ms]

Esercizio 2 :
Un condensatore inizialmente scarico, di capacità C = 50 μF,
viene caricato mediante un generatore di tensione avente
f.e.m. E = 25 V. Misurando la tensione all’istante t1= 0,2 s
si trova il valore V1 = 20 V. Calcolare la costante di tempo e
la resistenza del circuito di carica
[Risultati: τ= 0,124 s; R = 2,48 kΩ]

Esercizio 3 : Per il sottostante circuito di figura, in cui il condensatore è inizialmente
scarico, calcolare: la costante di tempo del circuito di carica; i valori finali
della tensione e dell’energia del condensatore; la corrente iniziale di carica;
la corrente i2 prima e dopo la chiusura del tasto T, disegnandone l’andamento.
[Risultati: ττ= 16 μs; μ Vf= 40 V; Wf= 32 μJ; Io= 0,1 A; prima della chiusura: I2= 20 mA,
costante;dopo la chiusura: i2 aumenta esponenzialmente da 0 a 20 mA]

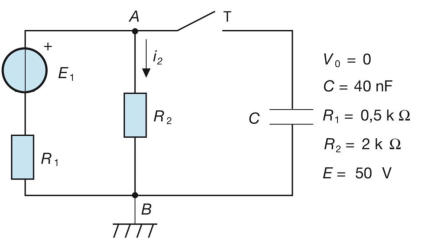
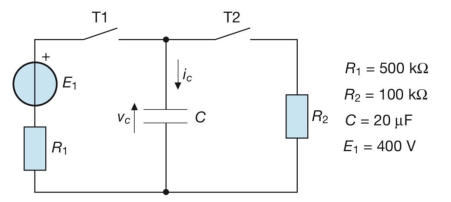
Esercizio 4 :
Nel sottostante circuito il condensatore è inizialmente carico con tensione Vo= 30 V e,
mediante la chiusura di T1 (con T2 aperto), viene caricato fino al raggiungimento del regime.
Successivamente, aprendo T1 e chiudendo T2, il condensatore viene completamente
scaricato sulla resistenza R3.
Per la prima fase del processo calcolare: la costante di tempo τ1; la tensione finale sul
condensatore; la corrente iniziale di carica; la variazione di carica elettrica sul condensatore;
l’andamento nel tempo della tensione v2.
Per la seconda fase del processo calcolare: la costante di tempo τ2; l’andamento della
corrente nel resistore R3; l’energia elettrica dissipata in R3.
[Risultati: τ1= 14 ms; Vf= 100 V; Io= 0,2 A; ΔQ = 2,8 mC; v2 diminuisce esponenzia-
-lmente da 30 V a zero; τ2= 20 ms; i3 diminuisce esponenzialmente da 0,2 A a zero;
WR3= 0,2 J]

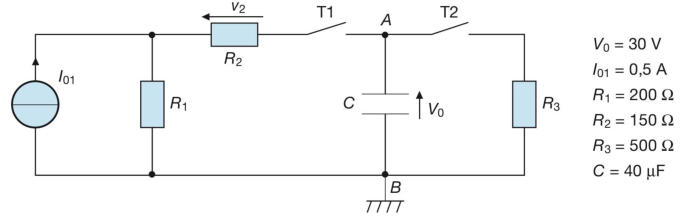
Esercizio 5 :
Nella sottostante rete il condensatore C è inizialmente scarico. Calcolare il valore della
corrente i3 con il tasto T aperto. Supponendo di chiudere T e di lasciare il circuito in tale
condizione, calcolare: la costante di tempo del circuito di carica, la corrente iniziale nel lato
capacitivo, la tensione sul condensatore e la corrente di carica al tempo t1 = 3 τ, il valore
finale della tensione sul condensatore, l’andamento della corrente i3 durante il transitorio
di carica. Disegnare gli andamenti della tensione vc e della corrente i3 in funzione del
tempo.
[Risultati: I3 = 0,18 A; τ = 13,8 μs; Io= 0,523 A; V1= 136,8 V; I1= 26 mA;
Vf= 144 V; andamento esponenziale crescente, da zero a 0,18 A]

Esercizio 6 :
Nel circuito di figura, il condensatore è inizialmente scarico. Il funzionamento del circuito è
il seguente: per i primi 30 s è chiuso T1 ed aperto T2; per i seguenti 10 s è aperto T1 e
chiuso T2; successivamente sono aperti ambedue gli interruttori.
Calcolare: la corrente iniziale di carica; la tensione vc dopo i primi 30 s; la corrente ic subito
prima e subito dopo la chiusura di T2; la tensione vc e la corrente ic al tempo finale di 40 s.
Disegnare gli andamenti di vc e ic in funzione del tempo.
[Risultati: Io= 0,8 mA; V1= 380 V; I1= 0,04 mA (prima) e I1= −3,8 mA (dopo);
V2 = 2,56 V; I2= −0,0256 mA]


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





