



Tenersi in punta di piedi non è crescere.
ELETTRONICA


… studiare, studiare ed ancora studiare,
è il solo modo di capire quanto possa
essere grande sia la propria ignoranza!
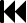

Massa
kilogrammo
kg
RISOLUZIONE DELLE RETI CAPACITIVE



Risoluzione delle reti capacitive a regime costante
Il comportamento a regime di una rete capacitiva può
essere studiato tenendo presente che, dopo il periodo
transitorio durante il quale i vari condensatori si caricano,
nella rete avvengono i seguenti fenomeni:
•
ogni condensatore rimane carico, con un valore di
tensione ai capi dipendente da come si ripartiscono le
tensioni imposte dai bipoli attivi presenti nella rete;
•
le correnti nei lati contenenti condensatori sono nulle,
in quanto, esaurito il transitorio di carica, non vi è più
flusso di cariche elettriche tra i vari condensatori e tra
questi e i generatori;
•
i generatori, essendo nulle le correnti, funzioneranno a
vuoto, a meno che non vi siano dei circuiti chiusi oltre
quelli costituiti dai condensatori;
•
sulle armature di ogni condensatore di capacità Ci si
stabilirà una carica elettrica Qi= Ci Vi dipendente dalla
tensione, positiva sull’armatura a potenziale elettrico
maggiore e negativa sull’altra
Esiste un’analogia tra le reti resistive e quelle capacitive; se si considerano le equazioni:
si nota che esse sono formalmente identiche se si rispettano le seguenti corrispondenze:
corrente
carica
I
Q
conduttanza
capacità G
C
tensione
tensione V
V
Essendo G = 1/R si avrà anche la corrispondenza R
1/C, dove la grandezza 1/C
(reciproca della capacità) è chiamata, in alcuni testi, elastanza.
Risolvere una rete capacitiva a regime costante significa, in generale, calcolare le
cariche parziali Qi, una per ogni lato della rete. Dato che ogni lato può comprendere
solo condensatori in serie (un parallelo di n condensatori corrisponde a n lati), aventi la
stessa carica, le cariche incognite sono, in ogni caso, pari al numero dei lati. Note le
cariche si calcolano le tensioni, con le espressioni Vi= Qi/Ci.
È valido anche il procedimento inverso: si risolve la rete calcolando le tensioni e da
queste si risale alle cariche, con le relazioni Qi= Ci Vi. Per far questo occorre, però,
ridurre gli eventuali condensatori in serie sui lati a quello equivalente, in modo da avere
sempre un numero di tensioni incognite pari a quello dei lati della rete.
Note le tensioni totali dei lati è facile risalire a quelle parziali della serie, mediante la
regola del partitore di tensione.
I metodi di risoluzione delle reti capacitive sono sostanzialmente gli stessi usati per
quelle resistive, ove si tenga conto dell’analogia illustrata in precedenza. I seguenti
esempi mostreranno l’applicazione dei metodi maggiormente usati.
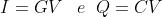








Esempio: Teorema di Millmann - Calcolare le tensioni e le cariche di ogni condensatore
della sottostante rete.
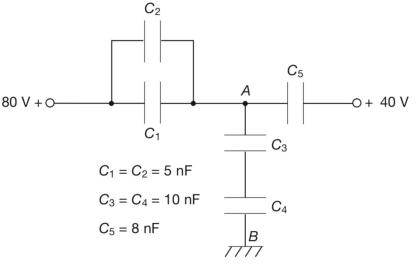
Riducendo i condensatori in parallelo C1-C2 e quelli in serie C3-C4 e inserendo i
generatori di tensione con f.e.m. E1= 80 V ed E2= 40 V, per tener conto delle
tensioni applicate tra i due estremi della rete e massa, si ottiene lo schema
semplificato di figura, dove:
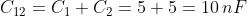
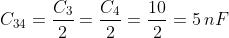
Il teorema di Millmann si applica alle reti resistive senza bipoli attivi di corrente nella
forma:
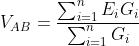
Per l’analogia conduttanza capacità, nel caso delle reti capacitive esso assumerà
invece la seguente forma

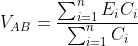
dove nella sommatoria al numeratore si deve tener conto delle polarità delle varie f.e.m.
rispetto al nodo A.
Nel caso in esame, con l’applicazione della soprastante relazione, si ricava:
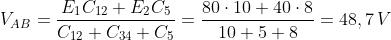
Essendo C3= C4 si avrà:
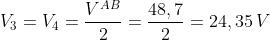
con polarità positiva verso il nodo A.
Poiché VAB < E1, per il lato di sinistra si avrà:
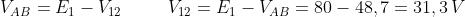
con polarità opposta a E1 (negativa verso il nodo A).
Il collegamento in parallelo tra C1 e C2 fa sì che sia:
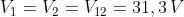
Poiché VAB > E2 , per il lato di destra si ha:
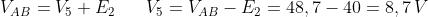
con polarità uguale a E2 (positiva verso il nodo A)
Note le tensioni, il calcolo delle cariche è immediato:
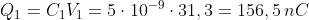
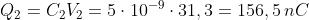
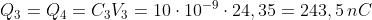
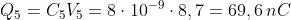

Esempio: Sovrapposizione degli effetti - Ripetere l’esempio precedente applicando il
principio di sovrapposizione degli effetti
L’applicazione della sovrapposizione degli effetti si svolge come per le reti resistive,
facendo agire separatamente i generatori. Gli schemi per il calcolo dei contributi di ogni
generatore sono rappresentati nelle figure a) e b).
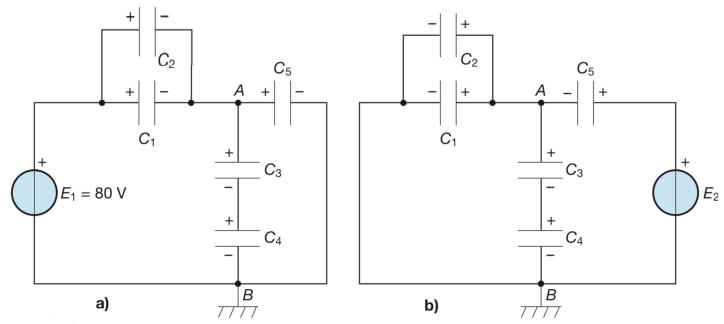
Il circuito di figura a) si può risolvere applicando ancora il teorema di Millmann; si ha:
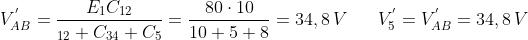
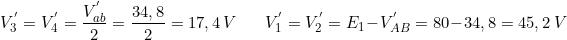
Con l’applicazione del teorema di Millmann si risolve anche il circuito di figura b)
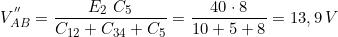
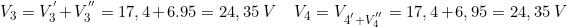
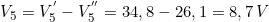

Esempio: Principi di Kirchhoff - Calcolare le cariche e le tensioni di ogni condensatore
della sottostante rete.
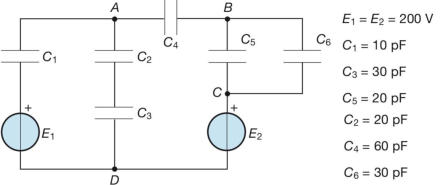
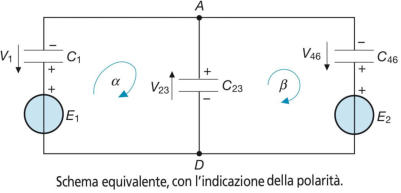
Per applicare i principi di Kirchhoff è opportuno che la rete venga ridotta a quella
equivalente, contenente un solo condensatore per lato, come nella sottostante figura.
Eseguendo le riduzioni, si ha:
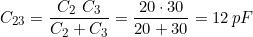
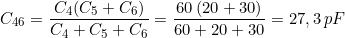
Se si tiene conto dell’equivalenza corrente <-> carica, il primo principio di Kirchhoff per
le reti capacitive si può formulare nel seguente modo: la somma algebrica delle cariche
sulle armature collegate a un nodo deve essere nulla.
Il secondo principio rimane lo stesso e può essere formulato come segue: la somma
algebrica delle tensioni lungo una maglia deve essere nulla.
Per applicare questo metodo si fissano arbitrariamente le polarità dei vari condensatori
e il verso di percorrenza delle maglie, si scrivono n–1 equazioni ai nodi e l–n+1
equazioni alle maglie e si risolve il relativo sistema.
Facendo riferimento al soprastante schema, si ha:
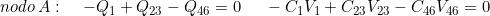
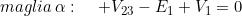
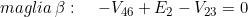
Sostituendo i valori noti si ottiene il sistema:
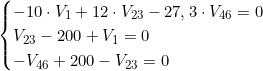
I risultati sono i seguenti (si omettono, per brevità, i passaggi matematici):
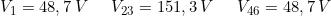
a cui corrispondono le cariche:
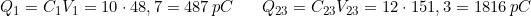
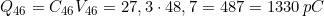
Essendo C2 e C3 collegati in serie si avrà:
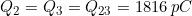
e quindi:
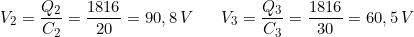
Anche C4 e C56 sono collegati in serie, per cui:
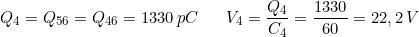
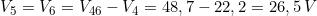


Esempio: Nel sottostante circuito calcolare il valore della capacità C1 , in modo che la
tensione di uscita sia Vu = 50 V
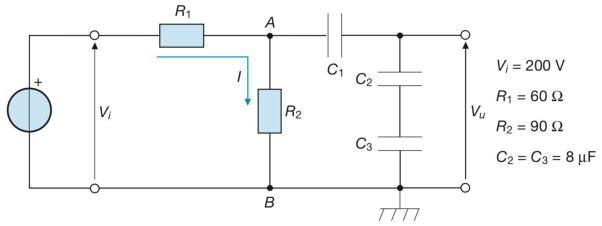
A regime, con i condensatori carichi, la corrente circola solo nella maglia contenente R1
e R2, tra loro in serie. La parte capacitiva della rete sarà quindi soggetta a una tensione
pari alla c.d.t. su R2, uguale a:
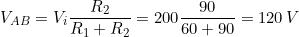
La tensione Vu è legata alla VAB dalla relazione:
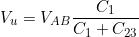
dove
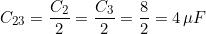
Sostituendo i valori noti e risolvendo l’equazione, si calcola il valore della capacità C1 :
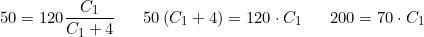
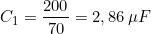


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





