



A che serve guadagnare trofei quando rinunci a essere te stesso?
OTTICA TEORICA
POLARIZZAZIONE CIRCOLARE

POLARIZZAZIONE CIRCOLARE
Si supponga ora che i due stati ortogonali
della apgina precedente abbiano una fase
relativa , cioè
Allora, se le corrispondenti ampiezze scalari sono eguali, se cioè ,le due
perturbazioni sono esprimibili tramite le funzioni
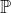
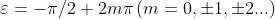
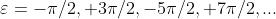
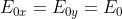
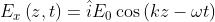
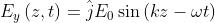
(il valore particolare di
fa semplicemente mutare la funzione coseno in una funzione seno).
L'onda risultante , è

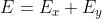
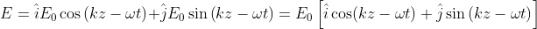
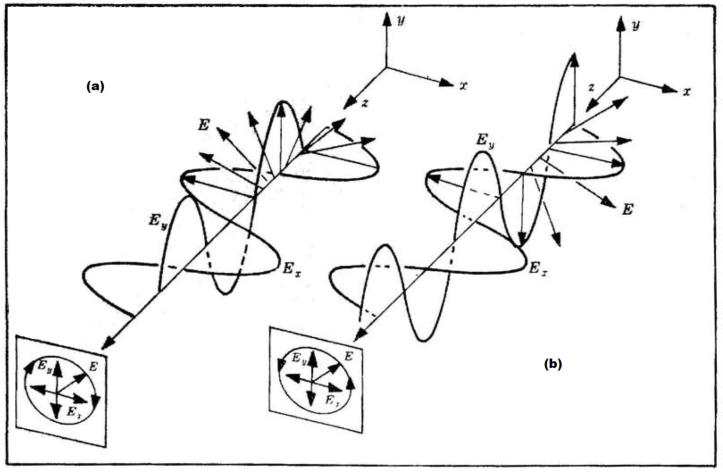
Il modulo (grandezza) di
è ed è costante, ma la direzione di
è una funzione
di z e t. Come nella soprastante figura (a), il vettore campo elettrico ruota in senso orario
(se si guarda verso la sorgente).
Dato che l'ampiezza è costante, la estremità di descrive un cerchio (per precisione,
una elica circolare) con una frequenza eguale a quella delle onde costituenti.
Un campo del genere è detto polarizzato circolare destro, corrispondente ad uno stato
.
Con un procedimento analogo, quando , il coseno
diventa un seno negativo, dando
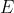
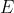
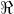
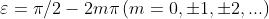
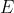
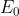

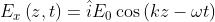
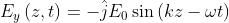
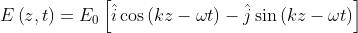
Anche in questo caso E ha un modulo costante, ma ora esso ruota in senso
antiorario (se si guarda verso la sorgente), come nella soprastante figura (b).
Il campo è polarizzato circolare sinistro, corrispondente ad uno stato
.
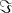
Gli stati
e
assumono una particolare importanza nella descrizione quantistica, nella
quale sono associati al momento angolare di spin dei fotoni. Tutti gli stati di polariz-
-zazione possono essere sintetizzati a partire dagli stati
e
. (vedi i problemi 5.11 e
5.21), un procedimento che è una necessità nel modello a fotoni.
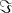
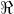
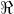
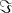

1 )
Descrivere la differenza tra l'onda di stato
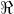
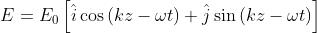
e un'onda di forma
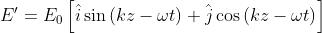
L'onda ha un modulo costante ed è polarizzata circolare. Si possono
facilmente confrontare le due perturbazioni esaminando il loro comportamento in un
qualche punto fisso dello spazio, ad esempio,
.
Per assume i valori
rispettivamente. Per questi stessi valori di t invece è eguale rispettivamente
a . Quindi è uno stato che per
è parallelo all'asse y.
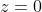
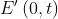
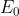
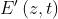
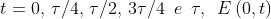
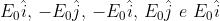
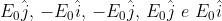
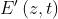
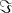
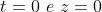

2)
Determinare lo stato di polarizzazione dell'onda
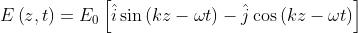
Il modulo di E, cioè , è anche in questo caso costante ed eguale ad , per
cui l'onda è circolare. Posto
, si esamini per
e si trova che assume rispettivamente i valori .
L'onda è evidentemente polarizzata circolare destra, dato che il campo E ruota in
funzione del tempo in senso orario.
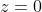
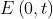
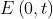
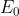
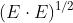
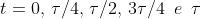
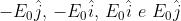

3)
Scrivere una espressione che rappresenti un'onda polarizzata circolare destra che
si propaga nella direzione delle z positive e tale che per il suo campo
E sia parallelo all'asse x e diretto nel verso negativo
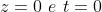
Dal problema 1)
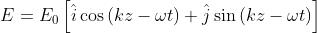
è in uno stato
diretto nel verso positivo delle x per . Ciò suggerisce
che l'onda richiesta dal presente problema abbia la forma
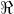
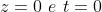
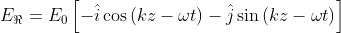
Come verifica, si veda cosa diventa per Per questi
valori diventa rispettivamente Essa è polarizzata
circolare destra ed ha una componente iniziale negativa nella direzione delle x
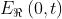
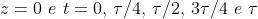
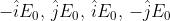

4)
Dimostrare che la sovrapposizione di uno stato e di uno stato dà uno stato
se i valori scalari delle ampiezze delle onde costituenti sono eguali.
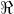
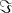
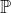
Scrivendo le due onde circolari come
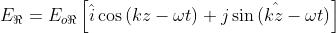
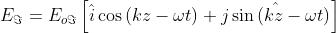
la loro somma diventa
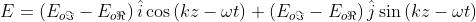
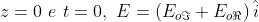
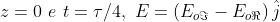
Si noti che per ,
mentre per
Dato che sia il modulo che la direzione di E variano in funzione di z e di t, l'onda
risultante non è polarizzata né linearmente né circolarmente.
Tuttavia se
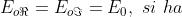
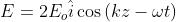
che è uno stato
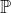

5)
Scrivere delle espressioni che rappresentino uno stato e uno stato che si
combinano dando uno stato .
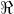
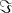
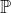
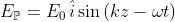
Tenendo presenti i tre problemi che precedono e il fatto che i termini coseno devono
elidersi, si considerino le espressioni
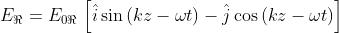
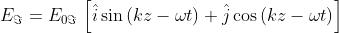
Dal problema 4) si sa che se si ha uno stato e quindi
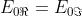
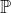
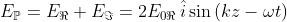
che è la espressione richiesta a condizione che sia
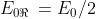

6)
Scrivere delle espressioni che rappresentino uno stato e uno stato che
sovrapposti diano uno stato che si propaga lungo l'asse z con il piano yz come
piano di vibrazione.
Le onde componenti devono evidentemente propagarsi nella direzione z. Si richiede
inoltre che il campo E giaccia nel piano yz per ogni valore di z e t. Ciò significa che E
deve avere solo una componente .
In base al problema 4) occorre anche che , che si pone eguale a
Se si sovrappongono uno stato inizialmente lungo l'asse x [cioè ]
e uno stato inizialmente lungo l'asse -x [cioè ]lo stato che ne
risulta inizia un ciclo all'ingiù. Ne segue, usando
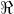
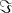
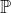
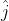
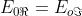
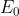
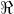
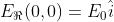
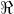
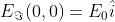
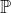
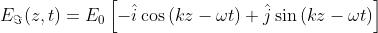
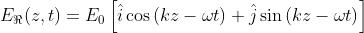
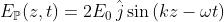
che
La scelta opposta (cioè lo stato ( inizialmente lungo -x e lo stato lungo x)
darebbe uno stato
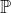
che inizia un ciclo all'insù. E' esattamente la soluzione opposta rispetto alla
precedente.

7)
Descrivere lo stato di polarizzazione dell'onda
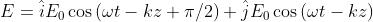
Sfruttando il fatto che si può riscrivere la
funzione d'onda nella forma
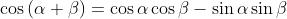
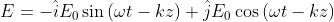
Per è uguale a
rispettivamente. Dato che il vettore campo ha lunghezza costante e ruota in
senso antiorario, l'onda è polarizzata circolare sinistra.
Un altro procedimento si ha usando il fatto che , mentre
. Ne segue che
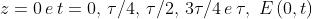
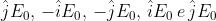
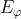
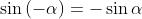
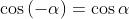
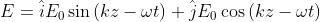
che si è già visto nel problema 1) essere uno stato
.


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





