



Una volta corre il cane e una volta la lepre
OTTICA TEORICA
IL PRINCIPIO DI FERMAT

IL PRINCIPIO DI FERMAT
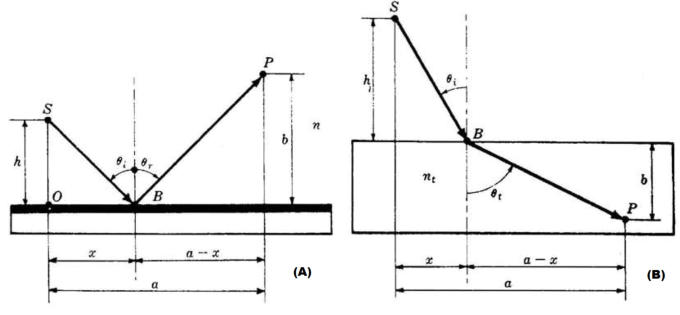
Circa duemila anni fa Erone di Alessandria affermava che un raggio di luce che proviene da
un punto S, si riflette su uno specchio ed arriva in un dato punto P, segue nello spazio il
percorso più breve possibile (figura A). Questa affermazione, vera nel caso di riflessione in
un mezzo omogeneo, non sarebbe vera per un raggio che parte da S, viene rifratto su una
interfaccia e arriva al punto P sempre nel secondo mezzo (figura B).
In questo caso il percorso più breve tra S e P è il segmento di retta SP, che non è certo il
percorso seguito dalla luce.
Nel 1657 Fermat generalizzò l'osservazione di Erone affermando che: un raggio di luce va
da un punto ad un altro seguendo il percorso per il quale impiega il tempo minore.
Benché generalmente vero, questo principio non è universalmente vero e deve essere in
parte modificato.
Si supponga che un raggio per andare da S a P percorra i tratti
in
mezzi rispettivamente di indici . Il tempo impiegato per compiere
l'intero percorso è:
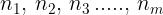
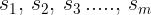
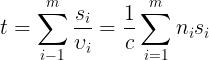
Questa ultima sommatoria è detta lunghezza del cammino ottico o O.P.L. (Optical
Path Length).
Il principio di Fermat può quindi essere riformulato nel seguente modo: un raggio di
luce segue il percorso che corrisponde alla più breve lunghezza del cammino ottico.
Per dare la formulazione più moderna e più generale del principio di Fermat, occorre
richiamare la nozione di valore stazionario di una funzione. Si dice che la funzione
f(x) ha in x= xo un valore stazionario, se la sua derivata df/dx è nulla per x=xo. Un valore
stazionario può corrispondere ad un massimo, ad un minimo o ad un punto di flesso
avente tangente orizzontale. In tutti i casi, f(x) in vicinanza di un valore stazionario f(xo)
varia lentamente, per cui
Si può ora esprimere così il principio di Fermat: un raggio di luce andando da un
punto ad un altro segue, quali che siano i mezzi attraverso i quali passa, un percorso che
corrisponde ad un valore stazionario della lunghezza del cammino ottico.
Questa formulazione si applica anche ai mezzi disomogenei per i quali si ha
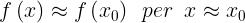
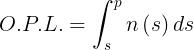
Il percorso effettivo è anche in questo caso quello per il quale la derivata di O.P.L. è
nulla. In termini fisici, il principio di Fermat può essere interpretato come un'affermazione
degli effetti della interferenza costruttiva. Ma su questo torneremo in seguito.

1 ) Spiegare come una formulazione alternativa del principio di Fermat sia: il percorso
effettivamente seguito da un raggio di luce è quello la cui O.P.L. è quasi eguale (cioè
eguale in prima approssimazione) alle lunghezze del cammino ottico dei percorsi
possibili ad esso vicini.
La validità della formulazione segue dal fatto che se Xo è un punto in cui f(x) è
stazionaria,
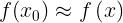
per valori di x tali che . In questo caso la funzione è la O.P.L.
Quindi il percorso effettivamente seguito dalla luce ha una O.P.L. stazionaria il cui valore
è quasi eguale alle lunghezze di cammino ottico dei percorsi vicini.
Un altro modo di affrontare lo stesso problema consiste nel rifarsi allo sviluppo in
serie di Taylor della funzione f(x). Fatto in un intorno di Xo dove
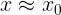
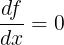
la serie di Taylor dà
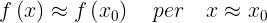
come ci si aspettava. L'espressione "in prima approssimazione" sta ad indicare il
fatto che la derivata seconda non è necessariamente nulla. Se si dovesse analizzare un
percorso possibile ma non effettivo (cioè non percorso effettivamente dalla luce), si
troverebbe che i percorsi ad esso adiacenti hanno valori di O.P.L. fortemente diversi.

2) Usare il principio di Fermat (nella sua formulazione matematica) per dedurre la
legge della riflessione

Come indicato nella soprastante figura (A), un raggio parte da S, colpisce l'interfaccia
in un punto B non meglio specificato e viene riflesso nel punto P. Assumendo che il
mezzo sia omogeneo e di indice n, si ha
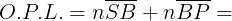
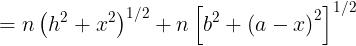
La O.P.L. è espressa come funzione della variabile x e la luce segue il percorso per
il quale
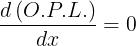
cioè
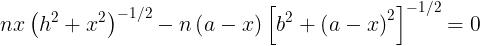
Ma ciò equivale a
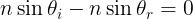
e quindi .
Quindi se un raggio va da S a P per riflessione in B, il principio di Fermat esige che
B sia collocato in modo tale che l'angolo di incidenza e l'angolo di riflessione siano
eguali
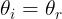

3) Applicare il principio di Fermat (nella sua formulazione matematica) alla rifrazione
per dedurre la legge di Snell.
Nella soprastante figura (B), un raggio va da S a P rifrangendosi nel punto B
dell'interfaccia. Si tratta di collocare B in modo tale che la derivata di O.P.L. sia nulla.
Si scrive perciò
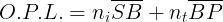
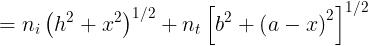
La variabile è x e quindi
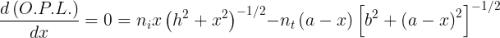
Questa espressione ha la forma , che equivale alla legge di
Snell. Il valore di x corrispondente ad un valore stazionario della O.P.L. è quello per il
quale vale la legge di Snell.
Altre posizioni di B corrispondono a valori diversi di x a nessuno dei quali corrisponde un
valore stazionario di O.P.L
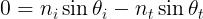

4) Usare la formulazione alternativa del principio di Fermat data nel sprastante problema
1) per arrivare senza calcolo alla legge di Snell.
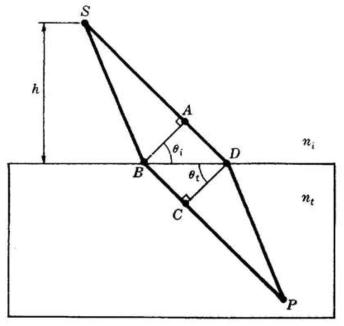
La figura destra mostra due raggi che vanno
entrambi da S a P. Le lunghezze del cammino
ottico di un raggio di luce reale relative a questi
due percorsi saranno quasi eguali se i due
percorsi sono abbastanza vicini. Di conseguenza,
assumendo che
siano piccoli
si ha che . Affinché le
lunghezze del cammino ottico
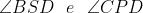
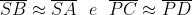
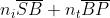
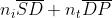
siano pressappoco eguali, occorre che
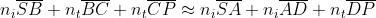
Ciò comporta che sia pressappoco eguale a . Se ora si pensa che
corrispondano a segmenti di fronti d'onda piani e .
L'approssimazione è buona a condizione che
sia molto piccolo. Infine allora
Il procedimento seguito in questo problema è forse matematicamente più semplice,
ma finisce per essere semplicistico,
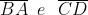
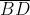
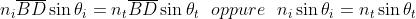
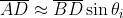
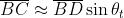
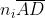
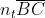

5) Un'onda sferica con origine in Spassa attraverso un arbitrario sistema ottico da cui
emerge come un'onda convergente in un punto P (come nella sottostante in figura).
Che cosa afferma il principio di Fermat per le lunghezze del cammino ottico dei vari
raggi che vanno da S a P?
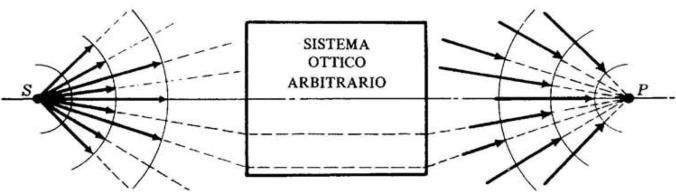

Si può presumere che i raggi che vanno da S a P seguano nel sistema ottico percorsi
molto diversi. Si supponga che uno di questi percorsi corrisponda al valore minimo di
O.P.L. tra S e P.
Il principio di Fermat afferma che la luce segue esattamente il percorso di O.P.L. minima
e non altri. Ma ovviamente occorre che siano seguiti anche altri percorsi, dato che i raggi
lasciano S secondo direzioni diverse.
Ne segue che non si può determinare in forma univoca un minimo (o un massimo) di
O.P.L. In altre parole ciò significa che tutti i raggi che vanno da Sa P passando attraverso
il sistema devono percorrere lunghezze di cammino ottico eguali. Ciò è vero per ogni tipo
di sistema di messa a fuoco (come lenti o specchi)

6) Un raggio collimato parallelo all'asse di simmetria di uno specchio concavo è riflesso
in un raggio convergente. Usando il principio di Fermat dimostrare che lo specchio
deve essere paraboloidale.
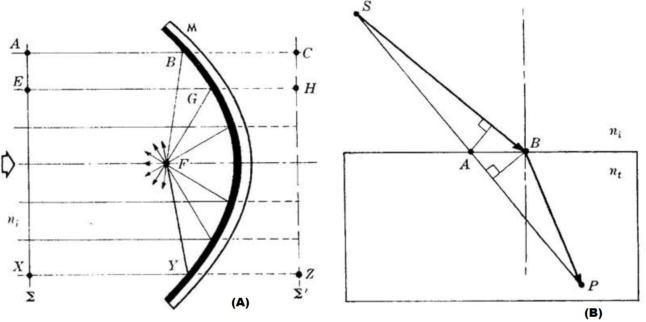
La soprastante figura (A)riporta, in sezione trasversale, raggi paralleli corrispondenti ad
una onda piana
che cadono sullo specchio M. I raggi riflessi convergono nel punto F.
Le lunghezze di cammino ottico di tutti i percorsi che vanno a finire in F devono essere
eguali (vedi precedentee problema con
).
Ne segue che
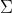
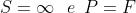
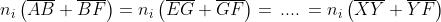
Si prolunghino ora i segmenti attraverso lo specchio fino nei punti
scelti in modo che
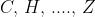
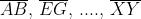
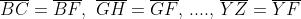
Le due serie di eguaglianze scritte comportano che
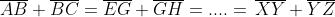
che equivale ad affermare che la distanza tra
e la linea
’ nei punti C, H, ... , Z è
una costante.
Si è quindi costruito una retta
' tale che i punti di M sono tutti equidistanti da essa e
dal punto F.
Per definizione quindi M è una parabola con fuoco in F e direttrice
’
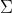
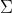
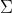
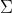

7) Si consideri un raggio di luce che parte da un punto S nell'aria e si rifrange in un
punto P nell' acqua, come nella soprastante figura (B). Dimostrare, usando il principio
di Fermat ma non la legge di Snell, che
.
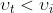
I raggi che lasciano S arrivano a P seguendo tutti un solo percorso,
. Ne segue
che la O.P.L. corrispondente deve essere un massimo o un minimo. Ma essa non
può essere un massimo dato che un raggio che ritornasse da P all'interfaccia e quindi
ancora in P avrebbe necessariamente una O.P L. molto maggiore. Ne segue che
è il valore minimo della O.P.L. Il cammino in linea retta ha
quindi una O.P.L maggiore. Dalla figura si ha e
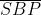
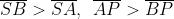
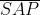
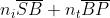
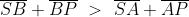
Quindi
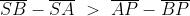
ed entrambi i membri della disuguaglianza sono grandezze positive. Inoltre
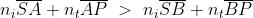
e quindi
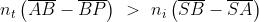
che significa che
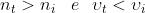
Ritornando alla figura (A) dell’ inizio del Principio di Fermat, dedurre il fatto che
usando il principio di Ferrnat, ma lasciando questa volta che la variabile spaziale sia
e non x.
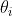
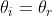

8)
Come in un precedente problema . Ma in questo caso
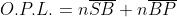
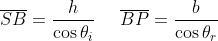
ne segue che
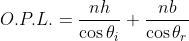
e derivando
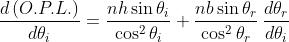
Quindi
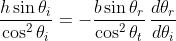
[1]
Dalla geometria del sistema si ha che sono vincolate dalla relazione
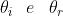
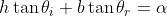
che derivando rispetto a , dà
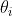
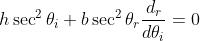
oppure
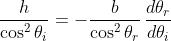
[2]
Dalle [1] e [2], cioè
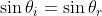
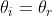


Lorem Ipsum Dolor
Cupidatat excepteur ea dolore sed in adipisicing id? Nulla lorem deserunt aliquip officia reprehenderit fugiat, dolor excepteur in et officia ex sunt ut, nulla consequat. Laboris, lorem excepteur qui labore magna enim ipsum adipisicing ut. Sint in veniam minim dolore consectetur enim deserunt mollit deserunt ullamco. Mollit aliqua enim pariatur excepteur. Labore nulla sunt, in, excepteur reprehenderit lorem fugiat. Ipsum velit sunt! Non veniam ullamco amet officia ut, ex mollit excepteur exercitation fugiat eu ut esse cupidatat in velit. Non eu ullamco in pariatur nisi voluptate mollit quis sed voluptate ea amet proident dolore elit. Occaecat nostrud dolore sunt, ullamco eu ad minim excepteur minim fugiat. Nostrud culpa eiusmod dolor tempor et qui mollit deserunt irure ex tempor ut dolore. Dolore, nostrud duis ad. In nulla dolore incididunt, sit, labore culpa officia consectetur mollit cupidatat exercitation eu. Aute incididunt ullamco nisi ut lorem mollit dolore, enim reprehenderit est laborum ut et elit culpa nulla. Excepteur fugiat, laboris est dolore elit. In velit lorem id, et, voluptate incididunt ut ad in sunt fugiat, esse lorem. Nisi dolore ea officia amet cillum officia incididunt magna nisi minim do fugiat ut nostrud dolore Qui in est in adipisicing ea fugiat aliqua. Reprehenderit excepteur laboris pariatur officia sit amet culpa aliquip quis elit eiusmod minim. Sint ut ut, proident in mollit do qui eu. Pariatur et cupidatat esse in incididunt magna amet sint sit ad, sunt cillum nulla sit, officia qui. Tempor, velit est cillum sit elit sed sint, sunt veniam.




© Irure ut pariatur ad ea in ut in et. In incididunt sed tempor





